yourdomain.com

Даны чашечные весы, имеющие особенность — они могут выдержать ровно 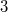взвешивания (неважно в каком порядке) неравных грузов, после чего ломаются. Одинаковые веса можно уравновешивать на этих весах бесконечное количество раз. Среди 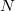монет есть одна фальшивая, вес которой меньше настоящих. Найдите максимальное 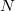при котором можно найти фальшивую не более, чем за 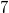взвешиваний на этих весах.
Нашёл решение для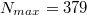 , строго обосновал и успокоился пока не узнал правильный ответ -
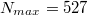. Какая-то хитрость применена, не могу догадаться какая.

Похоже или что-то не то с условиями или с ответом.
Для 379 несложно решить, первый раз надо по 73 взвешивать.
Ну и для общего случая - сколько всего взвешиваний и сколько неравновесных допустимо тоже знаю решение - типа паскалевского треугольника.
А вот 527 в нём всего один раз встречается - если ровно одно неравновесное взвешивание, а всего не более 263

СергейП писал(а):Source of the post
Похоже или что-то не то с условиями или с ответом.

Ответы на головоломки в IQ-календаре 2013 «Профессор» 5. Май.
[url=http://stprofessor.ru/filosofiya/otvety-na-golovolomki/]http://stprofessor.ru/filosofiya/otvety-na-golovolomki/[/url]

Интересно посмотреть решение для которого у тебя лично IQ недостаточен.

Вместо 3 и 7 берём соответственно и . Соответствующее максимальное значение обозначим . При каждом взвешивании либо не меняется либо уменьшается на единицу, а уменьшается на 1. Отсюда очевидна рекуррентность: - похоже на треугольник Паскаля.
Краевые условия: .

bot писал(а):Source of the post Вместо 3 и 7 берём соответственно и . Соответствующее максимальное значение обозначим . При каждом взвешивании либо не меняется либо уменьшается на единицу, а уменьшается на 1. Отсюда очевидна рекуррентность: - похоже на треугольник Паскаля.
Краевые условия: .

Ага!
Именно так и заполнил табличку в кселе минут за 5.
Ещё добавлю - количество взвешиваемых на каждой чашке камней -

СергейП писал(а):Source of the post
Именно так и заполнил табличку в кселе минут за 5.

Я тоже заполнил:

Если взвешивание равновесное, двигаемся вправо, в противном случае вниз.
Но как найти решение для ?

Таланов писал(а):Source of the post
Но как найти решение для ?

По реккурентности очевидно максимум. А что по ней такое число не вылазит? Ну, тогда так тому и быть - никак.

PS. Реккурентность приведёт к многочлену степени от переменной .

Таланов писал(а):Source of the post Я тоже заполнил:

Если взвешивание равновесное, двигаемся вправо, в противном случае вниз.
Но как найти решение для ?

То что заполнил - хорошо, но если бы ещё при этом стало понятно о чём речь - было бы ещё лучше.
Вот табличка о которой шла речь
В столбце А кол-во взвешиваний, а в 1-ой строке - допустимое число неравновесных взвешиваний.
На пересечении - максимальное
Искомое число в ячейке E9.

bot писал(а):Source of the post

Таланов писал(а):Source of the post
Но как найти решение для ?

По реккурентности очевидно максимум. А что по ней такое число не вылазит? Ну, тогда так тому и быть - никак.

Нам голову морочат и быть такого не может?