Задание с параметром
Добавлено: 10 сен 2013, 17:49
При каких значениях  уравнение имеет ровно три корня?
уравнение имеет ровно три корня?
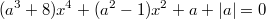
Неясен алгоритм действий. Скажем, если раскрывать модуль по определению: (a3+8)x4+(a2-1)x2+2a=0 и (a3+8)x4+(a2-1)x2=0. И что дальше? Если пытаться решить через дискриминант с помощью замены(x2=t) подобные уравнения, то ничего не выходит
Неясен алгоритм действий. Скажем, если раскрывать модуль по определению: (a3+8)x4+(a2-1)x2+2a=0 и (a3+8)x4+(a2-1)x2=0. И что дальше? Если пытаться решить через дискриминант с помощью замены(x2=t) подобные уравнения, то ничего не выходит