Многоугольник
Добавлено: 20 июн 2013, 23:12
DarkMel
У выпуклого 24-угольника стороны и диагонали окрашены либо в цвет
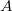
, либо в цвет

.
Вопрос: всегда ли возможно взять 4 вершины так, чтобы все стороны и диагонали полученного 4-угольника были окрашены в один цвет?
Какие есть мысли? Как доказать, что такое может быть всегда?
У нас 252 диагонали..
Верно ли то, что худший случай для нас - это когда 12 сторон в один цвет, 12 - в другой и 126 диагоналей в один цвет, 126 - в другой? Если да, то нужно ли это в задаче? Как доказать?
Используется теория графов или нет? Уже второй день никакой
Многоугольник
Добавлено: 21 июн 2013, 08:02
Ian
Лемма про 6-угольник и 3 вершины надо взять (она носит имя, к сожалению забыл. А по нему и решение этой задачи в сети найдется)
Возьмем вершину а, ребра в остальные 5 -как минимум 3 одного цвета, пусть для определенности это цвет А. Тогда 1) если между этими тремя есть ребро цвета А, то вместе с а это ребро дает искомый треугольник 2) если между этими тремя нет ребра цвета А, то они образуют треугольник цвета В
Ну а это обобщение леммы с 6=3! на 24=4!
Многоугольник
Добавлено: 21 июн 2013, 09:28
СергейП
Ian писал(а):Source of the post ...она носит имя, к сожалению забыл. А по нему и решение этой задачи в сети найдется...
Я вот тоже имя не могу вспомнить, но помнится что это венгр.
Можно по венгерским математикам поискать
Многоугольник
Добавлено: 21 июн 2013, 09:42
Ian
Многоугольник
Добавлено: 24 июн 2013, 08:51
DarkMel
Спасибо! Я смотрел теорему Рамсея.. Тут вот как получается.. Число Рамсея характеризует минимально возможный полный граф, чтобы выполнялись условия задачи. Это 18. А у нас 24 - хватит за глаза.
Но видимо, это-то и надо доказать, не опираясь на информацию извне. Ведь точно найти число Рамсея сложно, но получить для него какую-то оценку должно быть легче.
Есть какие-то идеи, как можно получить оценку? И с чего начать вообще..
Многоугольник
Добавлено: 24 июн 2013, 10:02
Hottabych
Многоугольник
Добавлено: 24 июн 2013, 19:50
DarkMel
А каким методом именно?.. С чего начать.. пока не могу разобраться, что тут кролик))
А если серьезно, то о какой оценке идет речь, я понимаю, что она есть, но не имею представления о механизме её получения.
Например, можно попробовать доказать, что R(4, 4)>17... как так сделать, чтобы довольно коротко получилось?
Многоугольник
Добавлено: 25 июн 2013, 06:57
Ian
Многоугольник
Добавлено: 26 июн 2013, 16:58
DarkMel
Мне кажется легче всего в этой задаче просто доказать, что
1)
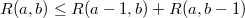
2)
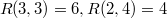
3) Из 1,2
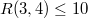
4) Из 1,3
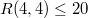
Вывод:
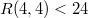
Многоугольник
Добавлено: 01 июл 2013, 18:21
arojda1
Если вопрос не потерял актуальность, могу доказать, что из 20 точек найдутся 4, соед. отрезками одного цвета.
Тут нужна будет ещё одна Лемма-2, следующая очевидным образом из упомянутой Леммы-1 о шести точках.
Только, для начала, немного терминологии, чтобы побыстрее. Назовём «связью типа А», если точки соед. отрезком цвета «А», ну и «В», соответственно. «Общество А» - 4 точки соединённые только отрезками цвета «А», и «В», соответственно.
Так вот, Лемма-2:
Если каждая из множества шести точек имеет «связь типа А» с какой-либо точкой вне множества и «связь типа В» с другой точкой вне этого множества, то среди этих восьми точек есть «Общество А» или «В», в зависимости от того, какого цвета там треугольник.
Теперь рассмотрим некую точку (назовём её – «Исходная точка»), имеющую «связь, например, типа А» с 10-ю точками. Каждая из этих десяти (пусть называется – «Вторая точка») точек имеет «связь типа А», как минимум, с четырьмя другими из оставшихся девяти. В противном случае, она имеет «связь типа В» с не менее, чем шестью точками этого множества, и приводит нас к Лемме-2.
Если какие-то две из этих четырёх точек имеют между собой «связь типа А», то мы имеем «общество А», состоящее из «исходной», «второй» и этих двух точек. Если нет, то мы имеем «общество В» из этих четырех точек.
DarkMel, 18 точек пока не одолел, но изначально, Вам, вроде, нужно было 24. И может кого-нибудь это натолкнёт на мысль, как разобраться с 18-ю.
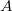 , либо в цвет
, либо в цвет  .
.