Теорема Мерсера
Добавлено: 03 авг 2011, 15:57
Существует ли многомерный аналог теоремы Мерсера?
То есть в каком случае справедливо разложение на![$$[a;~b]^4$$ $$[a;~b]^4$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Ba%3B~b%5D%5E4%24%24) :
:

для симметричного по всем переменным непрерывного ядра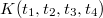 .
.
То есть в каком случае справедливо разложение на
для симметричного по всем переменным непрерывного ядра