Замечательная задача от П. Е. Пушкаря и К. Л. Шейнерман

Xenia1996 · Сообщение **Xenia1996** » 14 июн 2011, 15:58

На ММО-2003 предлагалась следующая задача:

Можно ли покрасить некоторые клетки доски 8×8 так, чтобы в любом квадрате 3×3 было ровно 5 закрашенных клеток, а в каждом прямоугольнике 2×4 (вертикальном или горизонтальном) – ровно 4 закрашенные клетки?

В предлагаемом автором решении доказывается, что нельзя раскрасить требуемым образом даже доску $6\times 6$ (а, следовательно, $8\times 8$ и подавно).

Я пошла дальше и доказала невозможность такой раскраски для доски $5\times 5$ и да возможность для доски $4\times 4$ .

Предлагаю уважаемым форумчанам попытаться повторить мой успех.

Xenia1996 · Сообщение **Xenia1996** » 14 июн 2011, 18:38

Ну, если тяжело $5\times 5$ , попробуйте хотя бы $4\times 4$ , это на порядок легче, всего лишь пример раскраски привести (в отличие от $5\times 5$ , где нужно доказать, что такая раскраска невозможна).

Equinoxe · Сообщение **Equinoxe** » 14 июн 2011, 19:02

Xenia1996 писал(а):Source of the post
Ну, если тяжело $5\times 5$ , попробуйте хотя бы $4\times 4$ , это на порядок легче, всего лишь пример раскраски привести (в отличие от $5\times 5$ , где нужно доказать, что такая раскраска невозможна).

Ну, раз никто не пишет, напишу я: элементарно доказать единственность раскраски для 4х4, тогда для 5х5 нужно перебрать всего две, каждая из которых невозможна.

СергейП

Xenia1996 писал(а):Source of the post Я ... доказала

Ну я тоже могу доказать.
Хотя красивость углядел только для доски $6\times 6$ .
Предположим, что закраска возможна, тогда расположив на доске 4 непересекающихся квадрата $3\times 3$ определяем, что должно быть покрашено $$20$$

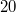
клеток.
А вот теперь самое любопытное - берем 4 прямоугольника $4\times 2$ и начинаем покрывать ими доску без перекрытий. Останутся незакрытыми 4 клетки. Так как в этих 4-х прямоугольниках 16 покрашенных клеток, значит все 4 незакрытых клетки покрашены!
Играем, двигая прямоугодьники по доске, получается, что незакрытыми могут быть только 5 блоков по $2\times 2$ клетки - в центре и по углам. Это в сумме дает 20 клеток, значит только они и должны быть покрашены. Проверяем выполнение условий - они не выполняются. Значит невозможно.
Там было подобное решение или иное?

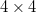
По доске $4\times 4$ пример раскраски привести совсем просто.

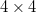
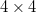
А вот для доски $5\times 5$ вышло долго, просто полный перебор показал, что закрытая спойлером раскраска единственная для доски $4\times 4$ , ну и разместить на доске $5\times 5$ в каждом квадрате $4\times 4$ такую покраску не получится.

Equinoxe писал(а):Source of the post элементарно доказать единственность раскраски для 4х4,

Хотелось бы посмотреть на это элементарное док-во

Xenia1996 · Сообщение **Xenia1996** » 14 июн 2011, 19:10

СергейП писал(а):Source of the post
Там было подобное решение или иное?

Это Вы про $6\times 6$ ?
Вот ссылка: [url=http://problems.ru/view_problem_details_new.php?id=105146]http://problems.ru/view_problem_details_new.php?id=105146[/url]

Equinoxe · Сообщение **Equinoxe** » 14 июн 2011, 19:16

СергейП писал(а):Source of the post
Equinoxe писал(а):Source of the post элементарно доказать единственность раскраски для 4х4,
Хотелось бы посмотреть на это элементарное док-во

Ну, это в принципе тоже перебор, но элементарный перебор. Будем смотреть, сколько занято клеток в центральном 2х2:
0. Тогда раскраска единственна и неверна
1. Тогда пары клеток сверху и снизу будут давать 1+2. Однако тогда неизбежно одному из 3х3 не хватит.
2. Тогда пары клеток -//- будут давать 0+2 или 1+1. Однако в обоих случаях одному 3х3 не хватит
3. Тогда пары клеток -//- будут 0+1, но в любом случае одному 3х3 не хватит.

P.S. чтобы увидеть элементарность сказанного, достаточно нарисовать рисунок (некий крестик такой). Я сначала на время доказывала (когда увидела ход мысли)
P.P.S. ура! у меня 239 сообщений — любимое число ^_^

Xenia1996 · Сообщение **Xenia1996** » 14 июн 2011, 19:22

Equinoxe писал(а):Source of the post
P.P.S. ура! у меня 239 сообщений — любимое число ^_^

Equinoxe · Сообщение **Equinoxe** » 14 июн 2011, 19:24

Xenia1996 писал(а):Source of the post
Equinoxe писал(а):Source of the post
P.P.S. ура! у меня 239 сообщений — любимое число ^_^

Так Вы из той самой 239-ой школы?

Xenia1996 · Сообщение **Xenia1996** » 14 июн 2011, 19:26

Equinoxe писал(а):Source of the post
Ох, если б я была из той самой… Нет, конечно Но ребят оттуда знаю, собственно, они и есть распространители любимости сего числа среди программистов

Xenia1996 · Сообщение **Xenia1996** » 14 июн 2011, 20:14

Только что нашла доказательство для $5\times 5$ , не использующее единственность раскраски доски $4\times 4$ .

А Вам слабо?

Правда, доказательство вышло длинное и нудное

yourdomain.com