Страница 1 из 1
Найти
Добавлено: 16 май 2011, 22:17
JeffLebovski
Найти
Добавлено: 16 май 2011, 22:35
Ellipsoid
Найти
Добавлено: 16 май 2011, 22:44
JeffLebovski
А что дальше?
Да кстати, он в элементраных вообще не считается вроде бы...
Что-то вообще ничего не понял, откуда

такое?
Найти
Добавлено: 16 май 2011, 22:46
Ellipsoid
Чушь написал. Пора спать ложиться. :lool:
Найти
Добавлено: 16 май 2011, 23:53
JeffLebovski
А если логарифм в ряд разложить? Стоит ли?
Найти
Добавлено: 17 май 2011, 00:29
ALEX165
Берите его по частям.
Найти
Добавлено: 17 май 2011, 06:45
Ian
Ответ
такойВ частности, это значит, что

но не вижу, как просто преобразовать один интеграл к другому

такая есть формула связи
Найти
Добавлено: 17 май 2011, 06:53
JeffLebovski
Я вообще попробовал его вычетами, сделал замену
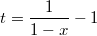
. Но ответа, который должен не получается. Получается вообще комплексный...
А смысл? Он в элементарных всё равно не берётся.
Найти
Добавлено: 17 май 2011, 08:13
BSK
Найти
Добавлено: 19 май 2011, 16:45
Dm13
Случайно всплыл в памяти фрагмент из "Вы конечно же шутите, мистер Фейнман" о том, как автор брал интегралы с помощью приёма введения параметра, который натолкнул на еще один вариант решения.
Обозначим
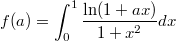
.
Тогда
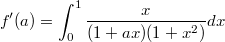
.
Раскладываем подинтегральное выражение на элементарные дроби:

.
Получаем:


.
Так как
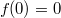
, то



.
Откуда,

.