yourdomain.com

Есть задача:

Маршрут разбит на 900 участков. Погрешность измерений длины каждого из них распределена по нормальному закону с нулевым средним и стандартным отклонением 5 метров. Найти, в каких пределах лежит суммарная погрешность с вероятностью 0.95.


Вероятность того, что абсолютная величина отклонения случайной величины X от ее
математического ожидания меньше некоторого малого положительного числа δ равна

, где-интегральная функция Лапласа.

По условию задачи

По таблице значений интегральной функции Лапласа находим, что




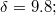
Это я нашел значение для одного участка.
Как мне теперь найти значение для всего маршрута ? То есть для 900 участков.
Может быть, это будет произведение 900*9.8 ?

Спасибо.

mat-maniak писал(а):Source of the post для 900 участков.
Может быть, это будет произведение 900*9.8 ?

По закону сложения дисперсий это будет 30*9,8

Ian писал(а):Source of the post

mat-maniak писал(а):Source of the post для 900 участков.
Может быть, это будет произведение 900*9.8 ?

По закону сложения дисперсий это будет 30*9,8

Спасибо большое! Ответ сошелся.
А где можно подробнее узнать о законе сложения дисперсий ?

mat-maniak писал(а):Source of the post
А где можно подробнее узнать о законе сложения дисперсий ?

Мм, везде! Дисперсия суммы независимых равна сумме дисперсий, т.е дисперсия Вашей суммы 900*25, теперь находим СКО суммы, далее как у Вас

спасибо !