Страница 1 из 6
Тригонометрические уравнения
Добавлено: 03 фев 2011, 18:05
Clever
Подскажите, пожалуйста, c чего начать решать это уравнение ?
(2sinx-cox)(1+cosx)=sin2x
Тригонометрические уравнения
Добавлено: 03 фев 2011, 18:29
AV_77
Как ни странно, но начать можно c раскрытия скобок.
Тригонометрические уравнения
Добавлено: 03 фев 2011, 19:00
myn
o! Придумала!
раскройте скобки, перенесите синус квадрат тоже в левую часть, c косинусом в квадрате они дадут 1. И потом сгруппируйте слагаемые - вынесите (1+cosx) за скобку.
получится
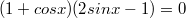
Тригонометрические уравнения
Добавлено: 03 фев 2011, 19:05
Hottabych
A может проще сразу

представить?
A еще лучше в тему для начинающих перебросить, a то начнут тут умные дяди и тети решать его c помощью какого нибудь интегрального преобразования упрощать?
Тригонометрические уравнения
Добавлено: 03 фев 2011, 19:10
myn
хитрый какой.. :acute: Сказано - раскрыть скобки! C модератором не поспоришь..
Тригонометрические уравнения
Добавлено: 03 фев 2011, 19:14
Hottabych
myn писал(а):Source of the post хитрый какой.. :acute: Сказано - раскрыть скобки! C модератором не поспоришь..
A c бывшим модератором можно?
Тригонометрические уравнения
Добавлено: 03 фев 2011, 19:56
myn
:ph34r: куда я попала..
Тригонометрические уравнения
Добавлено: 06 фев 2011, 12:57
Clever
Большое всем спасибо!
2cos2x+4cosx=3sin2x
2cos2x+4cosx-3(1-cos2x)=0
2cos2x+4cosx-3+3cos2x=0
5cos2x+4cosx-3=0
Д=16+60=76
У меня корень не извлекается, подскажите, пожалуйста, где я допускаю ошибку ?
Тригонометрические уравнения
Добавлено: 06 фев 2011, 13:07
Таланов
Извлеките приближённо.
Тригонометрические уравнения
Добавлено: 06 фев 2011, 16:34
myn
a зачем извлекать? Достаточно, думаю, дать просто ответ в виде арккосинуса. Я, по крайней мере, именно такие вижу ответы в учебниках.

Можно для пущей важности показать, что, т.к. это выражение приблизительно равно 0,472<0,5, то угол будет чуть больше +/- 60 градусов или

.