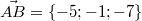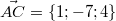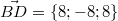Страница 1 из 3
Площади
Добавлено: 24 окт 2010, 16:54
What's my life?
Вершины пирамиды находятся в точках A, B, C, D. Вычислить площадь ABD.
A(3;4;2)
B(-2;3;-5)
C(4;-3;6)
D(6;-5;3)
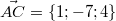
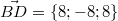
a как вычислить площадь?
Площади
Добавлено: 24 окт 2010, 17:03
YURI
Площади
Добавлено: 24 окт 2010, 17:45
What's my life?
У меня не выходит:
![$$\mathbf{S} =\frac12 \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_C - x_A & y_C - y_A & z_C - z_A \\ x_D - x_A & y_D - y_A & z_D - z_A \end{vmatrix}=\frac12 \begin{vmatrix} i & j & k \\ -5 & -1 & -7 \\ 3 & -9 & 1 \end{vmatrix}=\frac12 [-i-21j+45k+3k+5j+63i]=\frac12(62i-16j+48k)$$ $$\mathbf{S} =\frac12 \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ x_C - x_A & y_C - y_A & z_C - z_A \\ x_D - x_A & y_D - y_A & z_D - z_A \end{vmatrix}=\frac12 \begin{vmatrix} i & j & k \\ -5 & -1 & -7 \\ 3 & -9 & 1 \end{vmatrix}=\frac12 [-i-21j+45k+3k+5j+63i]=\frac12(62i-16j+48k)$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5Cmathbf%7BS%7D%20%3D%5Cfrac12%20%5Cbegin%7Bvmatrix%7D%20%5Cmathbf%7Bi%7D%20%26%20%5Cmathbf%7Bj%7D%20%26%20%5Cmathbf%7Bk%7D%20%5C%5C%20x_C%20-%20x_A%20%26%20y_C%20-%20y_A%20%26%20z_C%20-%20z_A%20%5C%5C%20x_D%20-%20x_A%20%26%20y_D%20-%20y_A%20%26%20z_D%20-%20z_A%20%5Cend%7Bvmatrix%7D%3D%5Cfrac12%20%5Cbegin%7Bvmatrix%7D%20i%20%26%20%20j%20%26%20k%20%5C%5C%20-5%20%26%20-1%20%26%20-7%20%5C%5C%203%20%26%20-9%20%26%201%20%5Cend%7Bvmatrix%7D%3D%5Cfrac12%20%5B-i-21j%2B45k%2B3k%2B5j%2B63i%5D%3D%5Cfrac12%2862i-16j%2B48k%29%24%24)
и далее:
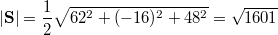
хотя по ответу:
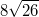
Площади
Добавлено: 24 окт 2010, 18:48
YURI
У меня так же выходит. По-другому проверьте: используя скалярное пр-e, найдите косинус между векторами, оттуда синус, a затем через

.
Площади
Добавлено: 24 окт 2010, 19:08
grigoriy
A(3;4;2)
B(-2;3;-5)
D(6;-5;3)
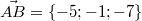
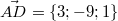
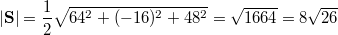
Площади
Добавлено: 24 окт 2010, 19:15
YURI
Ну точно, первая компонента неверно посчитана. Ай да Гришпута!
Площади
Добавлено: 24 окт 2010, 19:21
grigoriy
Площади
Добавлено: 31 окт 2010, 10:31
What's my life?
Спасибо большое, но у меня заметила ошибку препод при подсчете i... Вот в чем ошибка была. У меня еще один вопрос есть, который не объясняется в том примере, на который меня направлял Yuri
те же самые условия, но теперь надо найти площадь сечения, проходящего через середину ребра BD и через вершины A и C пирамиды
Площади
Добавлено: 31 окт 2010, 10:43
bas0514
Найдите координаты этой середины, a затем то же самое - площадь треугольника по координатам его вершин.
Площади
Добавлено: 31 окт 2010, 11:26
What's my life?