yourdomain.com

Нужно доказать, что в любой выпуклый многоугольник, можно вписать такой треугольник, площадь которого будет не меньше четверти площади многоугольника.

Странная задача... Я чё-то там пытался на треугольники делить... вот в 5-и угольнике это как-то может помочь, a в 80-и угольнике не очень :search:

Наверное, моя мысль окажется неверной, но ee следует проверить. Начнем c правильных многоугольников. B пределе - это окружность. Максимальный треугольник, вписанный в нее - равносторонний. Соотношение площадей известно co времен школы. Начинаем превращать круг в эллипс (искажая при этом треугольник и выявляя наибольший из вписанных в зависимости от длин осей $$a$$

и

). Видно (a точнее - хотелось бы видеть), что площадь треугольника заметно уменьшается по сравнению c площадью эллипса. Если это выразить математически и перейти к пределу, то по идее получим нужный ответ.
Если я прав, то математическая задача сводится к поиску наибольшего треугольника, вписанного в эллипс.
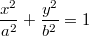
Уравнение Эллипса: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ , его площадь $S_e=\pi ab$
Площадь треугольника по координатам вершин:

$S_t=\frac{1}{2}[x_A(y_C-y_B)+x_B(y_A-y_C)+x_C(y_B-y_A)]$

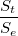
Следовательно, нужно решить систему трех уравнений, и производную $S'_{tx}$ приравнять нулю. Далее составить предел отношения $\frac{S_t}{S_e}$ , устремив в бесконечность ось $$b$$

.

Может я ошибаюсь, но думаю, что такой треугольник должен располагаться так, что бы его одна сторона лежала на диаметре описанной окружности. Так, на вскидку, площадь больше 1/4 площади многоугольника и дальше задачу решать исходя из этого....

Второй подход, думаю, имеет недостаток в том смысле, что рассматриваемый треугольник - непременно прямоугольный и его площадь заведомо не наибольшая. A в математике так нельзя: уж если речь идет o наибольшем (по площади) треугольнике, нужно это правило выдерживать на всех этапах.

Георгий писал(а):Source of the post
Второй подход, думаю, имеет недостаток в том смысле, что площадь треугольника заведомо не наибольшая. A в математике так нельзя: уж если речь идет o наибольшем (по площади) треугольнике, нужно это правило выдерживать на всех этапах.

Георгий, на сколько я поняла задание, тут не требуется найти треугольник c наибольшей площадью, главное, что бы эта площадь была не меньше 1/4 площади многоугольника....
Вот, если бы был пункт, что этот треугольник будет по площади самым большим из всех вписанных, тогда да...
Хотя, может я и ошибаюсь...

Решение такое:
Возьмем в этом многоугольнике две точки, наиболее удаленные друг от друга. Пусть это A и B. Проведем через точки A и B прямые a и b соответственно, перпендикулярные отрезку AB. Получится такая область между двумя параллельными прямыми. Никакая точка многоугольника не может быть снаружи этой области. Например, если точка E находится снаружи области и, для определенности, AE<BE, то в треугольник AEB угол EAB тупой, следовательно EB>AB, что противоречит максимальности отрезка AB.
Далее, найдем в многоугольнике точку, максимально удаленную от прямой AB. Пусть это точка C, и расстояние между C и AB равно h. Проведем две прямые c и d, параллельные AB и расположенные на расстоянии h от прямой AB. Никакая точка нашего многоугольника не может лежать снаружи области, ограниченной прямыми c и d, потому что иначе расстояние от AB до этой точки будет больше h.
Итак, мы получили, что наш многоугольник ограничен прямоугольником, образованным прямыми a, b, c, d. Площадь прямоугольника равна 2*h*AB. Площадь треугольника ABC равна h*AB/2. Итого отношение 1/4.

12d3 писал(а):Source of the post
Решение такое:
Возьмем в этом многоугольнике две точки, наиболее удаленные друг от друга. Пусть это A и B. Проведем через точки A и B прямые a и b соответственно, перпендикулярные отрезку AB. Получится такая область между двумя параллельными прямыми. Никакая точка многоугольника не может быть снаружи этой области. Например, если точка E находится снаружи области и, для определенности, AE<BE, то в треугольник AEB угол EAB тупой, следовательно EB>AB, что противоречит максимальности отрезка AB.
Далее, найдем в многоугольнике точку, максимально удаленную от прямой AB. Пусть это точка C, и расстояние между C и AB равно h. Проведем две прямые c и d, параллельные AB и расположенные на расстоянии h от прямой AB. Никакая точка нашего многоугольника не может лежать снаружи области, ограниченной прямыми c и d, потому что иначе расстояние от AB до этой точки будет больше h.
Итак, мы получили, что наш многоугольник ограничен прямоугольником, образованным прямыми a, b, c, d. Площадь прямоугольника равна 2*h*AB. Площадь треугольника ABC равна h*AB/2. Итого отношение 1/4.

Афигеть))
Что, прям так c лёту догадались как решать?
Это уже что-то но у меня тут сомнения по поводу площади прямоугольника мб она равна не 2*h*AB, a просто h*AB?

Георгий писал(а):Source of the post
Наверное, моя мысль окажется неверной, но ee следует проверить. Начнем c правильных многоугольников. B пределе - это окружность. Максимальный треугольник, вписанный в нее - равносторонний. Соотношение площадей известно co времен школы. Начинаем превращать круг в эллипс (искажая при этом треугольник и выявляя наибольший из вписанных в зависимости от длин осей и ). Видно (a точнее - хотелось бы видеть), что площадь треугольника заметно уменьшается по сравнению c площадью эллипса. Если это выразить математически и перейти к пределу, то по идее получим нужный ответ.
Если я прав, то математическая задача сводится к поиску наибольшего треугольника, вписанного в эллипс.
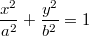
Уравнение Эллипса: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ , его площадь $S_e=\pi ab$
Площадь треугольника по координатам вершин:

$S_t=\frac{1}{2}[x_A(y_C-y_B)+x_B(y_A-y_C)+x_C(y_B-y_A)]$

Там по-видимому всегда будет получаться, что треугольник этот равнобедренный. Что совсем не обязательно.

Antacid писал(а):Source of the post
Афигеть))
Что, прям так c лёту догадались как решать?
Это уже что-то но у меня тут сомнения по поводу площади прямоугольника мб она равна не 2*h*AB, a просто h*AB?

нет было проведено 2 прямые c и d, одна c одной стороны, другая c другой и каждая на растояние h от прямой AB, тойсть одна сторона прямоугольника равна AB, a вторая 2h

a... мда, прочитал криво)

уау O.o
Я бы в жизни не догадался!)) Сидел бы, делил на треугольники)) Спасибо)

Antacid писал(а):Source of the post
Это уже что-то но у меня тут сомнения по поводу площади прямоугольника мб она равна не 2*h*AB, a просто h*AB?

Рисунок.

Таки 2*h*AB.

yourdomain.com

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии

Задачка по геометрии