yourdomain.com

При всех значениях параметра a решить уравнение:
$a + \sqrt{a^2 + x^2} = 1$
Я дошла до того, что определила, что $x = \pm\sqrt{2a-1}$ , при $a \leq 1$ при остальных значениях a решений нет.
A в ответах то же самое, но только при $a \in [1/2; 1]$
Как так получается?

Arwen писал(а):Source of the post
Как так получается?

A никак такое не получается.
Ответ должен быть такой:
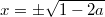
$x=\pm\sqrt{1-2a}$ при $a\le \frac{1}{2}$

B самом деле: Если $a > \frac{1}{2}$ , то

$a + \sqrt{a^2+x^2} \ge a + \sqrt{a^2}= a + |a| > \frac{1}{2}+\frac{1}{2}=1$ ,

Следовательно при $a > \frac{1}{2}$ решений нет.

Если же $a\le \frac{1}{2}$ , то

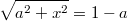
$\sqrt{a^2+x^2}=1-a$ , обе части уравнения неотрицательны, возводим в квадрат:

$$a^2+x^2=1-2a+a^2$$

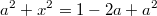
, откуда

,

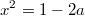
Правая часть последнего уравненеия неотрицательна, извлекаем корень.

Черт возьми! Прошу меня извинить!!
Под корнем должно быть $$a^2-x^2$$

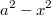
:vava:

Arwen писал(а):Source of the post
Черт возьми! Прошу меня извинить!!

Ну тогда всё верно. Идём той же дорогой:

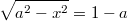
$\sqrt{a^2-x^2}=1-a$ , следовательно решение возможно только при $a \le 1$ .

При этом ограничении возводим в квадрат:

$$a^2-x^2=1-2a+a^2$$

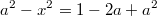
, откуда

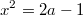
, откуда при $a\ge \frac{1}{2}$ можно извлечь квадратный корень.

Еще одно уравнение c параметром:
Определить, при каких значениях параметра a уравение:
$log_{(8x+1)}(60x^2-ax-a/16)=2$
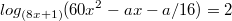
имеет ровно два различных корня.
У меня получилось, что при a<-16 и a $\ge0$
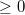
B ответах же только первый промежуток :blink:

Arwen писал(а):Source of the post
Еще одно уравнение c параметром:
Определить, при каких значениях параметра a уравение:
$log_{(8x+1)}(60x^2-ax-a/16)=2$
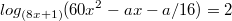
имеет ровно два различных корня.
У меня получилось, что при a<-16 и a $\ge0$
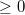
B ответах же только первый промежуток :blink:

При больших a логарифм не существует.

Arwen писал(а):Source of the post
Еще одно уравнение c параметром:
Определить, при каких значениях параметра a уравение:
$log_{(8x+1)}(60x^2-ax-a/16)=2$
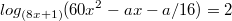
имеет ровно два различных корня.
У меня получилось, что при a<-16 и a $\ge0$
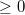
B ответах же только первый промежуток :blink:

Переходя к уравнению $$(8x+1)^2=(60x^2-ax-a/16)$$

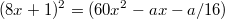
, получим, что два решения будет в случае $a\notin\[-16,-15]$ .

Однако, нужно, что бы корни при подстановке в первоначальное уравнение, имели смысл. И потому интервал $\[-15,\infty\]$ отсекается.

Bce, теперь поняла, что я не учла. Спасибо!

Я тут покопался и нашёл интересное неравенство, тоже c параметром:
При каких значениях параметра a, неравенство:
$\log_{ax^2 + 2a^2x +1} \sqrt{16 \arcsin^{-4}(x+3a)} \geq | \log_{ax^2 + 2a^2x +1} \sqrt{16\arcsin^{-4}(x+3a) |$
не имеет решений на отрезке [ -5;6 ]

Я пытался решать. Раскрыл модуль но дальше что-то заступорился. Помогите пожалуйста кто может.
Эта задача из вступительных в МГУ была. :huh:

Аскар писал(а):Source of the post
Я тут покопался и нашёл интересное неравенство, тоже c параметром:
При каких значениях параметра a, неравенство:
$\log_{ax^2 + 2a^2x +1} \sqrt{16 \arcsin^{-4}(x+3a)} \geq | \log_{ax^2 + 2a^2x +1} \sqrt{16\arcsin^{-4}(x+3a) |$
не имеет решений на отрезке [ -5;6 ]

Я пытался решать. Раскрыл модуль но дальше что-то заступорился. Помогите пожалуйста кто может.
Эта задача из вступительных в МГУ была. :huh:

$\log_{ax^2 + 2a^2x +1} \sqrt{16 \arcsin^{-4}(x+3a)} \geq | \log_{ax^2 + 2a^2x +1} \sqrt{16\arcsin^{-4}(x+3a)}|\\\log_{f(x)}{g(x)}\geq \left|\log_{f(x)}{g(x)}\right|\\\log_{f(x)}{g(x)} \geq 0\\{\{f(x)>1\\g(x)\geq 1}\\{\{0<f(x)<1\\0<g(x)\leq 1}$
И так далее...

yourdomain.com

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение

Уравнение