Доказать неравенство
Добавлено: 01 ноя 2016, 11:00
Здраствуйте. Возникла у меня затыка в курсовой по рядам. Там в одной задаче я исследовала числовой ряд на сходимость, доказала, что он сходится, а вот для его абсолютной сходимости пришлось доказывать одно промежуточное неравенство. Неравенство такое:
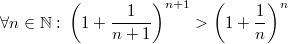 .
.
С виду просто, поэтому и поместила в школьную математику. Попробовала с помощью мат.индукции, получаются такие громоздкие выкладки, что сама в них запуталась. Как доказать? Неравенство вроде очевидное.. Присоветуйте, пжлст.
С виду просто, поэтому и поместила в школьную математику. Попробовала с помощью мат.индукции, получаются такие громоздкие выкладки, что сама в них запуталась. Как доказать? Неравенство вроде очевидное.. Присоветуйте, пжлст.