Подчёркиваю, что для рациональной степени не понятен этот вопрос. Жду ответ, поскольку исходная задача оказалась для меня очень полезной Хочу использовать её в качестве иллюстрации для одной проблемы.TR63 писал(а):Source of the post Всё-таки не понятно, где в доказательстве неравенства Бернулли используется обязательно(?) второй замечательный предел.
Доказать неравенство
Доказать неравенство
Последний раз редактировалось TR63 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать неравенство
Неравенство Бернулли для произвольной вещественной степени доказывается через поиск минимума функцииTR63 писал(а):Source of the post Всё-таки не понятно, где в доказательстве неравенства Бернулли используется обязательно(?) второй замечательный предел.
Вот этот момент надо довести до конца и посмотреть, как инструменты будут использоваться. Потому что если будет использоваться производная степенной функции с ненатуральным показателем, опять замкнутый круг получается.TR63 писал(а):Source of the post Можно проверить, что многочлен f(x) имеет в области положительных (x) только один кратный корень
Последний раз редактировалось 12d3 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать неравенство
12d3, Ваши пояснения относятся к действительному показателю в неравенстве Бернулли.. Мой вопрос касался именно рационального показателя. Задача мною сведена к исследованию многочлена с натуральным показателем. Там всё элементарно. Для решения исходного неравенства достаточно применить неравенство Бернулли с рациональныи показателем. Вы этот вариант забраковали, сказав, что будет обязательно ( почему?) использоваться второй замечатеьный предел. Но это для действительного показателя. В нашей задаче в исходном неравенстве рациональный показатель. Задача о неравенстве Бернулли с рациональным показателем сведена к исследованию многочлена с натуральным показателем. Берёте производную и видите, что многочлен имеет только один положительный кратный корень. (Где Вы видите у многочлена действительную степень. Посмотрите внимательнее. Она натуральная.) Отрицательные корни нас не интересуют. И в моём доказательстве нет никакого второго замечательного предела. Из того, что он был при действительном показателе вовсе не должно обязательно следовать его наличие при рациональном показателе. А, Вы это утверждали, бракуя метод, предложенный в начале темы. Но Вашего обоснования для рационального показателя (а, именно о таком идёт речь; в исходной задаче никаких действительных показателей нет), я не вижу.TR63 писал(а):Source of the post TR63 в 05.11.2016, 09:43 написал(а): linkВсё-таки не понятно, где в доказательстве неравенства Бернулли используется обязательно(?) второй замечательный предел. Подчёркиваю, что для рациональной степени не понятен этот вопрос.
Последний раз редактировалось TR63 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать неравенство
TR63, покажите это. Мне, например, это совсем не очевидно.TR63 писал(а):Source of the post
Можно проверить, что многочлен f(x) имеет в области положительных (x) только один кратный корень.
Последний раз редактировалось ARRY 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать неравенство
Здесь 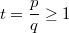 , (p;q)-натуральные.
, (p;q)-натуральные.

 ,
, 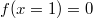 , значит корень
, значит корень 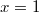 кратный.
кратный.
С учётом количества перемен знака положительных корней не более двух. Отсюда и следует, что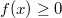 (для конкретных (p;q) для контроля можно проверить на вольфраме). Что и требовалось доказать, т.к. в f(x) всегда можно подставить
(для конкретных (p;q) для контроля можно проверить на вольфраме). Что и требовалось доказать, т.к. в f(x) всегда можно подставить 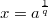 , где
, где 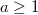 , и получить, что неравенство Бернулли верно для любой рациональной степени
, и получить, что неравенство Бернулли верно для любой рациональной степени 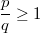 .
.
Если выкладки верны, то при желании можно пристегнуть матиндукцию. Но это уже будет излишне.
С учётом количества перемен знака положительных корней не более двух. Отсюда и следует, что
Если выкладки верны, то при желании можно пристегнуть матиндукцию. Но это уже будет излишне.
Последний раз редактировалось TR63 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать неравенство
Спасибо, теперь видно, что все верно.
Последний раз редактировалось 12d3 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Доказать неравенство
Да, вроде как всё правильно. А индукция тогда уже и не нужна.TR63 писал(а):Source of the post Если выкладки верны,
Последний раз редактировалось ARRY 27 ноя 2019, 17:52, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 2 гостей