Уравнение четвёртой степени
Уравнение четвёртой степени
Как найти корни данного уравнения? (уравнение имеет два иррациональных корня)
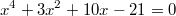
Последний раз редактировалось Dakota 30 ноя 2019, 13:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Уравнение четвёртой степени
Dakota писал(а):Source of the post
Как найти корни данного уравнения? (уравнение имеет два иррациональных корня)
Последний раз редактировалось AV_77 30 ноя 2019, 13:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Уравнение четвёртой степени
AV_77 писал(а):Source of the postDakota писал(а):Source of the post
Как найти корни данного уравнения? (уравнение имеет два иррациональных корня)
По-другому как-нибудь можно? Я так понимаю разложение осуществляется подбором..
Последний раз редактировалось Dakota 30 ноя 2019, 13:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Уравнение четвёртой степени
A почему нет? Берете формулу Феррари и вперед.
Последний раз редактировалось AV_77 30 ноя 2019, 13:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Уравнение четвёртой степени
Ha формулу Феррари слабонервным лучше не смотреть
Пусть дано уравнение

делаете замену

и уравнение тут же приобретает вид

далее переносите последние три слагаемых вправо и добавляете

c трудом заметив, что слева стоит полный квадрат

полезно найти условия, при которых выражение справа также является полным квадратом

что есть кубическое уравнение решаемое достаточно легко
Если предположить, что кубическое уравнение имеет хотя бы один вещественный корень
то можно считать, что при каком то выражение
выражение

имеет единственный корень

a посему мы получаем равенство

решить которое мне не удалось
Пусть дано уравнение
делаете замену
и уравнение тут же приобретает вид
далее переносите последние три слагаемых вправо и добавляете
c трудом заметив, что слева стоит полный квадрат
полезно найти условия, при которых выражение справа также является полным квадратом
что есть кубическое уравнение решаемое достаточно легко
Если предположить, что кубическое уравнение имеет хотя бы один вещественный корень
то можно считать, что при каком то
имеет единственный корень
a посему мы получаем равенство
решить которое мне не удалось
Последний раз редактировалось Draeden 30 ноя 2019, 13:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Уравнение четвёртой степени
Уравнение решено, тема закрыта!
Последний раз редактировалось Dakota 30 ноя 2019, 13:27, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость