Поэтому уравнение имеет решение только при положительных h и отрицательных значениях k.
Возможно ли решить уравнение?
Возможно ли решить уравнение?
Поэтому уравнение имеет решение только при положительных h и отрицательных значениях k.
Последний раз редактировалось vicvolf 28 ноя 2019, 19:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Возможно ли решить уравнение?
В общем, если сформулировать задачу полностью. Есть формула разложения по Лапласу (переход от изображения к функции времени):

соответственно мое уравнение имеет вид:

Со свободной составляющей (первый член) все понятно, подставляем нуль вместо p. Производную от знаменателя тоже можно найти, для второго члена, а вот решение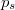 находим относительно
находим относительно
W(p)=0
если в знаменателе заменить

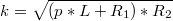
при этом
nl=a+jb
Раскрываем знаменатель
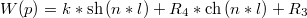
и раскрывая гиперболические функции от nl получаем комплексное число, где и мнимая и действительная часть должны быть нулем
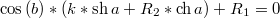
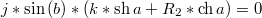
оно распадается на два, решаем первое когда синус равен нулю, то есть b=s*pi, тогда и получается наше уравнение
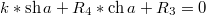
А дальше у меня пошли затруднения. То есть мы в конечном счете должны получить возрастающую функцию от нуля (по экспоненте), которая переходит в вынужденную (первый член, график параллельно оси t)
соответственно мое уравнение имеет вид:
Со свободной составляющей (первый член) все понятно, подставляем нуль вместо p. Производную от знаменателя тоже можно найти, для второго члена, а вот решение
W(p)=0
если в знаменателе заменить
при этом
nl=a+jb
Раскрываем знаменатель
и раскрывая гиперболические функции от nl получаем комплексное число, где и мнимая и действительная часть должны быть нулем
оно распадается на два, решаем первое когда синус равен нулю, то есть b=s*pi, тогда и получается наше уравнение
А дальше у меня пошли затруднения. То есть мы в конечном счете должны получить возрастающую функцию от нуля (по экспоненте), которая переходит в вынужденную (первый член, график параллельно оси t)
Последний раз редактировалось Opas 28 ноя 2019, 19:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Возможно ли решить уравнение?
Ну вот теперь все гораздо проще - перед гиперсинусом  нету А значит уравнение вполне решается аналитически. Нужно перейти к двойному углу:
нету А значит уравнение вполне решается аналитически. Нужно перейти к двойному углу: 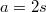 , затем увеличить степень до двух:
, затем увеличить степень до двух:  и преобразовать
и преобразовать  - получаем однородное уравнение. Делим на
- получаем однородное уравнение. Делим на  и получаем квадратное уравнение относительно
и получаем квадратное уравнение относительно  . Дальше сами сможете
. Дальше сами сможете
Умножение пишется \cdot
И по-моему зря Вы от комплексного уравнения
Перешли к действительному: это уравнение решается точно так же, как я выше написал, только чуть сложнее из-за .
.
(я только строго выкладки не проверял)
Умножение пишется \cdot
И по-моему зря Вы от комплексного уравнения
Перешли к действительному: это уравнение решается точно так же, как я выше написал, только чуть сложнее из-за
(я только строго выкладки не проверял)
Последний раз редактировалось Sonic86 28 ноя 2019, 19:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Возможно ли решить уравнение?
Я немного намудрил с набором, сейчас переправил
Последний раз редактировалось Opas 28 ноя 2019, 19:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Возможно ли решить уравнение?
У меня еще такой вопрос к специалистам по математике:
если у уравнения комплексные корни, как их находить?
если у уравнения комплексные корни, как их находить?
Последний раз редактировалось Opas 28 ноя 2019, 19:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Возможно ли решить уравнение?
Так же как и действительные. Или вы про что-то другое спрашиваете?
Последний раз редактировалось AV_77 28 ноя 2019, 19:24, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 9 гостей