Разложил на множители разность кубов
Ещё одно уравнение с заменой переменной
Ещё одно уравнение с заменой переменной
Разложил на множители разность кубов
Последний раз редактировалось Таланов 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
В посте 10 мы пришли к кубическому уравнению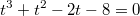
Я Вам говорил, что есть такая теорема Безу [url=http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%...E0_%C1%E5%E7%F3]http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%...E0_%C1%E5%E7%F3[/url]
У которой есть полезное следствие - Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
У нас как раз слева многочлен, удолетворяющий данным свойствам. Делители его свободного члена -+1,-1,+2,-2. Если их подставить в уравнение, то мы обнаружим, что t=2, как я писал в посте 10 является корнем кубического уравнения.
Теорема Безу утверждает что остаток от деления многочлена P(x) на двучлен x − a равен P(a). Если а является корнем уравнения. то P(a)=0 и в этом случае P(x) делится на x − a без остатка. Следовательно надо разделить многочлен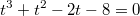 на одночлен t-2. Делить многочлен на многочлен Вы умеете? Это делается вот так [url=http://ipo.spb.ru/iumk2/MATH_XXI-10/Module....2/M_1.2.2.html]http://ipo.spb.ru/iumk2/MATH_XXI-10/Module....2/M_1.2.2.html[/url]
на одночлен t-2. Делить многочлен на многочлен Вы умеете? Это делается вот так [url=http://ipo.spb.ru/iumk2/MATH_XXI-10/Module....2/M_1.2.2.html]http://ipo.spb.ru/iumk2/MATH_XXI-10/Module....2/M_1.2.2.html[/url]
После деления мы получаем действительно многочлен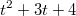 и соответственно квадратное уравнение относительно t
и соответственно квадратное уравнение относительно t 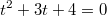
Почему я столько пишу об этом, так как это действительно важный метод для решения уравнения со степенью 3 и выше, но к сожалению в школьном курсе ему уделено мало места. Конечно в данном случае можно делать, как сказано в посте 21, но в общем случае так не получится!
Дальше вы решаете квадратное уравнение и находите еще 2 решения t2 и t3, но они получаются комплексными, поэтому действительным решением является только t1=2.
Решая уравнение
 мы получаем единственный действительный корень x=1. Надо добавить, что область изменения функции
мы получаем единственный действительный корень x=1. Надо добавить, что область изменения функции  в действительной области (-бесконечность,-2], [2, +бесконечность).
в действительной области (-бесконечность,-2], [2, +бесконечность).
Я Вам говорил, что есть такая теорема Безу [url=http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%...E0_%C1%E5%E7%F3]http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%...E0_%C1%E5%E7%F3[/url]
У которой есть полезное следствие - Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
У нас как раз слева многочлен, удолетворяющий данным свойствам. Делители его свободного члена -+1,-1,+2,-2. Если их подставить в уравнение, то мы обнаружим, что t=2, как я писал в посте 10 является корнем кубического уравнения.
Теорема Безу утверждает что остаток от деления многочлена P(x) на двучлен x − a равен P(a). Если а является корнем уравнения. то P(a)=0 и в этом случае P(x) делится на x − a без остатка. Следовательно надо разделить многочлен
После деления мы получаем действительно многочлен
Почему я столько пишу об этом, так как это действительно важный метод для решения уравнения со степенью 3 и выше, но к сожалению в школьном курсе ему уделено мало места. Конечно в данном случае можно делать, как сказано в посте 21, но в общем случае так не получится!
Дальше вы решаете квадратное уравнение и находите еще 2 решения t2 и t3, но они получаются комплексными, поэтому действительным решением является только t1=2.
Решая уравнение
Последний раз редактировалось vicvolf 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
Таланов писал(а):Source of the post
Разложил на множители разность кубови вынес за скобку общий множитель.
Теперь понял, спасибо.
vicvolf писал(а):Source of the post
В посте 10 мы пришли к кубическому уравнению
Я Вам говорил, что есть такая теорема Безу [url=http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%...E0_%C1%E5%E7%F3]http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%...E0_%C1%E5%E7%F3[/url]
У которой есть полезное следствие - Свободный член многочлена делится на любой целый корень многочлена с целыми коэффициентами (если старший коэффициент равен 1, то все рациональные корни являются и целыми).
У нас как раз слева многочлен, удолетворяющий данным свойствам. Делители его свободного члена -+1,-1,+2,-2. Если их подставить в уравнение, то мы обнаружим, что t=2, как я писал в посте 10 является корнем кубического уравнения.
Теорема Безу утверждает что остаток от деления многочлена P(x) на двучлен x − a равен P(a). Если а является корнем уравнения. то P(a)=0 и в этом случае P(x) делится на x − a без остатка. Следовательно надо разделить многочленна одночлен t-2. Делить многочлен на многочлен Вы умеете? Это делается вот так [url=http://ipo.spb.ru/iumk2/MATH_XXI-10/Module....2/M_1.2.2.html]http://ipo.spb.ru/iumk2/MATH_XXI-10/Module....2/M_1.2.2.html[/url]
После деления мы получаем действительно многочлени соответственно квадратное уравнение относительно t
Почему я столько пишу об этом, так как это действительно важный метод для решения уравнения со степенью 3 и выше, но к сожалению в школьном курсе ему уделено мало места. Конечно в данном случае можно делать, как сказано в посте 21, но в общем случае так не получится!
Дальше вы решаете квадратное уравнение и находите еще 2 решения t2 и t3, но они получаются комплексными, поэтому действительным решением является только t1=2.
Решая уравнениемы получаем единственный действительный корень x=1. Надо добавить, что область изменения функции
в действительной области (-бесконечность,-2], [2, +бесконечность).
Спасибо большое. По-поводу того, что данной теореме уделяется слишком мало времени в школьном курсе, должен не согласиться. В моей школе ей вовсе не уделялось внимание, так что я о ней услышал впервые на этом форуме:).
Ну а теперь я ещё весь следующий день буду разбираться с алгоритмом решения, который вы здесь описали. Хоть вы всё и изложили довольно подробно, но моему не тренированному уму придётся изрядно постараться, чтобы всё это усвоить.
Последний раз редактировалось modesto 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
modesto писал(а):Source of the post Ну а теперь я ещё весь следующий день буду разбираться с алгоритмом решения, который вы здесь описали.
Оставьте немного времени, чтобы разобраться вот с этим
При
Отрицательных корней нет, т.к. при
Последний раз редактировалось BSK 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
BSK писал(а):Source of the postmodesto писал(а):Source of the post Ну а теперь я ещё весь следующий день буду разбираться с алгоритмом решения, который вы здесь описали.
Оставьте немного времени, чтобы разобраться вот с этим
Присумма в кажой скобке не меньше 2, поэтому есть только один положительный корень
Это действительно так, но требует у ТС также времени для доказательства
Последний раз редактировалось vicvolf 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
modesto писал(а):Source of the post
Спасибо большое. По-поводу того, что данной теореме уделяется слишком мало времени в школьном курсе, должен не согласиться. В моей школе ей вовсе не уделялось внимание, так что я о ней услышал впервые на этом форуме:).
Я тоже о ней ничего не знаю. Но ведь удалось решить вашу задачу.
Последний раз редактировалось Таланов 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
Таланов писал(а):Source of the postmodesto писал(а):Source of the post
Спасибо большое. По-поводу того, что данной теореме уделяется слишком мало времени в школьном курсе, должен не согласиться. В моей школе ей вовсе не уделялось внимание, так что я о ней услышал впервые на этом форуме:).
Я тоже о ней ничего не знаю. Но ведь удалось решить вашу задачу.
Ну с Вашим то нестандартным способом мышления (по сравнению с моим) и огромным опытом это вполне закономерно;)
Последний раз редактировалось modesto 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Ещё одно уравнение с заменой переменной
Да бросьте, вы. Это как раз стандартный приём.
Последний раз редактировалось Таланов 28 ноя 2019, 20:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей