Мне эта задачка показалась ну очень простой. Буквально первая идея привела к решению. А Вы как считаете?
Задачка с индийской математической олимпиады
Задачка с индийской математической олимпиады
Найти все функции  .
.

Мне эта задачка показалась ну очень простой. Буквально первая идея привела к решению. А Вы как считаете?
Мне эта задачка показалась ну очень простой. Буквально первая идея привела к решению. А Вы как считаете?
Последний раз редактировалось Equinoxe 28 ноя 2019, 21:00, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
неправильное решение:
Последний раз редактировалось Sonic86 28 ноя 2019, 21:00, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
Первое что пришло в голову: f(u)=u. Осталось найти остальные решения
Последний раз редактировалось Ludina 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
Запишем 2 уравнения (переименовывая переменные):


Из которых:
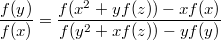
Обращаем внимание, что отношение справа не должно зависить от z. Такие же соотношения получаются для остальных двух переменных. Делаем вывод:
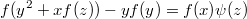
(или не делаем - пишу "по первому впечатлению")
И вот 2 варианта ответа:
f(x)=x;
f(x)=0.
Может, еще что-то есть...
Из которых:
Обращаем внимание, что отношение справа не должно зависить от z. Такие же соотношения получаются для остальных двух переменных. Делаем вывод:
(или не делаем - пишу "по первому впечатлению")
И вот 2 варианта ответа:
f(x)=x;
f(x)=0.
Может, еще что-то есть...
Последний раз редактировалось Ludina 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
Ludina писал(а):Source of the post
Запишем 2 уравнения (переименовывая переменные):
Из которых:
Обращаем внимание, что отношение справа не должно зависить от z. Такие же соотношения получаются для остальных двух переменных. Делаем вывод:
(или не делаем - пишу "по первому впечатлению")
И вот 2 варианта ответа:
f(x)=x;
f(x)=0.
Может, еще что-то есть...
Ага, именно они. Решала по-другому — представила, что x=z=0, а дальше всё по маслу
Последний раз редактировалось Equinoxe 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
Объясните мне вот это место, плиз
Это неверно. Возьмите
Уравнение эквивалентно
Последний раз редактировалось Sonic86 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
Хм, Вы правы, есть ещё как минимум f(1)=const.
Сейчас поищу
Последний раз редактировалось Equinoxe 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
Последний раз редактировалось Sonic86 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
А хорошая идея, кстати. Отсюда видно, что решением уравнения
Последний раз редактировалось bas0514 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с индийской математической олимпиады
На основании того, что 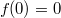 ,
, 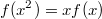 , и откидывая случай
, и откидывая случай 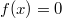 - константа.
- константа.
1)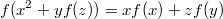
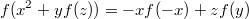
Значит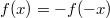
2) Предположим что есть - отличное от нуля, такое что
- отличное от нуля, такое что 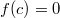
Положим , получим
, получим 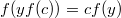
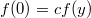 откуда
откуда 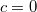 .
.
3) Положим , получим
, получим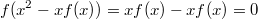
Или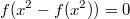
Значит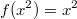
На основании пункта 1: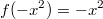
Тоесть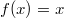
Проверьте плиз)
1)
Значит
2) Предположим что есть
Положим
3) Положим
Или
Значит
На основании пункта 1:
Тоесть
Проверьте плиз)
Последний раз редактировалось MrDindows 28 ноя 2019, 21:01, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 33 гостей