А кто, кто нашёл-то?
Задачка с Белорусской олимпиады
Задачка с Белорусской олимпиады
А кто, кто нашёл-то?
Последний раз редактировалось Таланов 28 ноя 2019, 21:09, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с Белорусской олимпиады
BSK писал(а):Source of the postНет, конечно. Но решение нигде и не опирается на то, что отрезок соединяющий середину оснований, является высотой.Equinoxe писал(а):Source of the post Возьмём произвольную трапецию с высотой = m+n, которую можно «вписать» в параболу. Подходит ли она под условие?
Я не к этому вела, а к тому, что если длина отрезка, соединяющего середины оснований, равна n+m, это ещё не означает, что рассматриваемая трапеция вообще подходит под вид, описываемый в условии.
Не доказывать это всё равно что не проверять, а можно ли вписать трапецию полученного вида в параболу, а затем говорить «А зачем проверять? Это же по условию сказано, что она вписана»
Последний раз редактировалось Equinoxe 28 ноя 2019, 21:09, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с Белорусской олимпиады
Вот всё решение
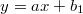 и
и 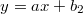 - уравнения оснований трапеции
- уравнения оснований трапеции
 и
и  - это проекции оснований на ось
- это проекции оснований на ось 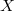
Т.к. отрезок, соединяющий середины оснований, перпендикулярен оси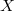 (убедитесь!), искомая площадь равна
(убедитесь!), искомая площадь равна
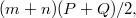
где
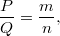
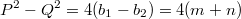
Т.к. отрезок, соединяющий середины оснований, перпендикулярен оси
где
Последний раз редактировалось BSK 28 ноя 2019, 21:09, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с Белорусской олимпиады
BSK писал(а):Source of the post
Вот всё решениеи
- уравнения оснований трапеции
и
- это проекции оснований на ось
Т.к. отрезок, соединяющий середины оснований, перпендикулярен оси(убедитесь!), искомая площадь равна
где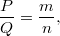
Вот теперь всё нормально
Последний раз редактировалось Equinoxe 28 ноя 2019, 21:09, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка с Белорусской олимпиады
Ну и слава Богу. Разобрались.
Последний раз редактировалось Таланов 28 ноя 2019, 21:09, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Школьная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость