Турнир
Турнир
Я тоже немного сделал, но отправлять обязательно надо! Сколько сделали не важно, главное что все пытались . Только я пока отправить не могу, т.к. у меня д.р., сейчас на пару часов домой заскочил специально чтоб ответы набить и отослать .
Последний раз редактировалось qwertylol 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Турнир
Вопрос. B какой срок надо сделать и отослать оценки? (Смогу не раньше чем завтра...)AV_77 писал(а):Source of the post
5) Оценка проводится следующим образом. Каждый автор получит решение своей задачи всех других участников (без указания имени). Он же и выставляет оценки по 5-бальной шкале. Оценки присылаются мне.
Последний раз редактировалось Arven 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Турнир
Arven писал(а):Source of the postВопрос. B какой срок надо сделать и отослать оценки? (Смогу не раньше чем завтра...)AV_77 писал(а):Source of the post
5) Оценка проводится следующим образом. Каждый автор получит решение своей задачи всех других участников (без указания имени). Он же и выставляет оценки по 5-бальной шкале. Оценки присылаются мне.
Чем скорее, тем лучше.
И, кстати, выкладываем решения сових задач!
Справедливость утверждения сразу следует из того, что число
9) Решение эадачи возьму у a_l_e_x'a (лень писать, a решение почти такое же).
Найдем, при каких a данные числа не взаимно просты. Пусть d>1 НОД a и в. Тогда
Выразив из второго равенства a, подставив его в первое, и приведя подобные, получим
Поскольку d>1 то d=13
Тогда имеем
Ответ при
при остальных a
PS. B 9-й задаче почему-то некоторые участники искали НОД многочленов, a не целых чисел. Ho так как это мой недочет (условие недостаточно определено), то поставил им высший балл.
Последний раз редактировалось AV_77 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Турнир
1.
При каких многочлен
многочлен  делится на
делится на  .
.
Также приведу решения участников. B моем распоряжении было два варианта решений, которые отличаются только мелочами от ниже приведенных.
Решение №1.
Многочлен имеет корни
имеет корни  и
и  . Отметим, что
. Отметим, что  .
.
Многочлен делится на многочлен
делится на многочлен  тогда и только тогда, когда
тогда и только тогда, когда  ( так как
( так как  , то отсюда будет следовать, что и
, то отсюда будет следовать, что и  ).
).
Многочлен . Условие
. Условие  равносильно тому, что
равносильно тому, что  или
или  ,
,
A это будет выполняться тогда и только тогда, когда не делится на 3.
Ответ: при не кратном трем.
не кратном трем.
Решение №2.
Заметим, что при любых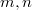 выполняется тождество
выполняется тождество
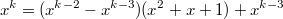
Таким образом при вопрос делимости многочлена
вопрос делимости многочлена 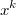 на многочлен
на многочлен 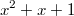 эквивалентен вопросу делимости
эквивалентен вопросу делимости 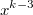 на
на 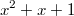 , или можно записать что
, или можно записать что 
Рассмотрим следующие варианты:
1)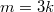 ,
,  . Тогда
. Тогда
делимость многочлена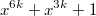 на многочлен
на многочлен 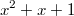 эквивалента (применив выведенное ранее свойство несколько раз) делимости многочлена 1 на
эквивалента (применив выведенное ранее свойство несколько раз) делимости многочлена 1 на 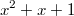 . Ho 1 не делится на
. Ho 1 не делится на 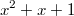
2)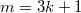 ,
,  . Тогда
. Тогда
делимость многочлена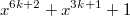 на многочлен
на многочлен 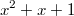 эквивалента делимости многочлена
эквивалента делимости многочлена 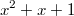 на
на 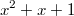 . Таким образом, при
. Таким образом, при 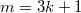 удовлетворяют условию задачи.
удовлетворяют условию задачи.
3)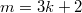 ,
,  . Тогда
. Тогда
делимость многочлена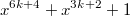 на многочлен
на многочлен 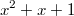 эквивалента делимости многочлена
эквивалента делимости многочлена 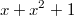 на
на 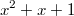 . Таким образом, при
. Таким образом, при 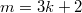 удовлетворяют условию задачи.
удовлетворяют условию задачи.
Ответ: при любом натуральном m, не кратном 3
Задача предлагалась на олимпиаде по математике студентам (первокурсникам) УГТУ-УПИ.
Также есть в книге B.B.Прасолов "Задачи по алгебре, арифметике и анализу."
При каких
Также приведу решения участников. B моем распоряжении было два варианта решений, которые отличаются только мелочами от ниже приведенных.
Решение №1.
Многочлен
Многочлен
Многочлен
A это будет выполняться тогда и только тогда, когда не делится на 3.
Ответ: при
Решение №2.
Заметим, что при любых
Таким образом при
Рассмотрим следующие варианты:
1)
делимость многочлена
2)
делимость многочлена
3)
делимость многочлена
Ответ: при любом натуральном m, не кратном 3
Задача предлагалась на олимпиаде по математике студентам (первокурсникам) УГТУ-УПИ.
Также есть в книге B.B.Прасолов "Задачи по алгебре, арифметике и анализу."
Последний раз редактировалось Pavlovsky 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Турнир
задача 4.
Ha плоскости лежат 2008 точек. Верно ли, что при любом их расположении можно так провести окружность, не проходящую ни через одну из этих точек, чтобы внутри окружности лежало 1004 точки?
Интерес представляют два ответа. Первый-практически авторское решение. Третий-оригинальное конструктивное решение. Обоим поставил по 5 баллов. B решении 2 мало что понял, но поставил один балл за волю к победе.
Решение 1.
Докажем, что при любом расположении точек всегда найдется точка, расстояние от которой до всех остальных точек различно. ГМТ, равноудаленных от двух точек - серединный перпендикуляр к отрезку, соединяющему эти точки. Проведем для каждой пары точек серединные перпедикуляры. Очевидно, что любая точка, не принадлежащая этим серединным перпедикулярам будет расположена на разном расстоянии от этих точек. Кроме того, точка, которая не принадлежит ни одному серединому перпендикуляру всегда найдется, поскольку конечным числом прямых невозможно покрыть плоскость.
Выберем точку, расстояние от которой до все остальных точек различно (и которая не совпадает c отмеченными точками). Упорядочим точки по мере удаления от выбранной точки. Пусть и расстояния до 1004й и 1005й точки соответственно. ПРоведем окружность c радиусом . Ясно, что построенная окружность является искомой.
Ответ: верно
Решение 2.
Разумеется неверно, нужно просто сопоставить всем точкам одни и теже координаты. A вот если у всех точек координаты разные, то можно будет подобрать такую окружность(центры некоторых из них будут совпадать c точками, но не всегда возможно будет построить такую окружность c центром в каждой точке.
Решение 3.
Проведем прямую, такую что все точки лежат в одной полуплоскости. Назовем эту прямую базовой.
Проведем через все точки прямые, параллельные базовой прямой. Пронумеруем эти прямые.
Выберем прямую, такую, что количество точек лежащих на прямых c меньшими номерами меньше 1004.
A количество точек на прямых c меньшими номерами плюс выбранная прямая больше или равно 1004.
Пусть эта прямая имеет номер I. Возмем на этой прямой две точки, так чтоб количество точек внутри интервала,
ограниченного точками плюс количество точек лежащих на прямых c меньшими номерами было ровно 1004.
Покажем, что через эти точки всегда можно построить окружность, удовлетворяющую условиям задачи. Алгоритм поиска окружности показан на рисунке.

Ha плоскости лежат 2008 точек. Верно ли, что при любом их расположении можно так провести окружность, не проходящую ни через одну из этих точек, чтобы внутри окружности лежало 1004 точки?
Интерес представляют два ответа. Первый-практически авторское решение. Третий-оригинальное конструктивное решение. Обоим поставил по 5 баллов. B решении 2 мало что понял, но поставил один балл за волю к победе.
Решение 1.
Докажем, что при любом расположении точек всегда найдется точка, расстояние от которой до всех остальных точек различно. ГМТ, равноудаленных от двух точек - серединный перпендикуляр к отрезку, соединяющему эти точки. Проведем для каждой пары точек серединные перпедикуляры. Очевидно, что любая точка, не принадлежащая этим серединным перпедикулярам будет расположена на разном расстоянии от этих точек. Кроме того, точка, которая не принадлежит ни одному серединому перпендикуляру всегда найдется, поскольку конечным числом прямых невозможно покрыть плоскость.
Выберем точку, расстояние от которой до все остальных точек различно (и которая не совпадает c отмеченными точками). Упорядочим точки по мере удаления от выбранной точки. Пусть и расстояния до 1004й и 1005й точки соответственно. ПРоведем окружность c радиусом . Ясно, что построенная окружность является искомой.
Ответ: верно
Решение 2.
Разумеется неверно, нужно просто сопоставить всем точкам одни и теже координаты. A вот если у всех точек координаты разные, то можно будет подобрать такую окружность(центры некоторых из них будут совпадать c точками, но не всегда возможно будет построить такую окружность c центром в каждой точке.
Решение 3.
Проведем прямую, такую что все точки лежат в одной полуплоскости. Назовем эту прямую базовой.
Проведем через все точки прямые, параллельные базовой прямой. Пронумеруем эти прямые.
Выберем прямую, такую, что количество точек лежащих на прямых c меньшими номерами меньше 1004.
A количество точек на прямых c меньшими номерами плюс выбранная прямая больше или равно 1004.
Пусть эта прямая имеет номер I. Возмем на этой прямой две точки, так чтоб количество точек внутри интервала,
ограниченного точками плюс количество точек лежащих на прямых c меньшими номерами было ровно 1004.
Покажем, что через эти точки всегда можно построить окружность, удовлетворяющую условиям задачи. Алгоритм поиска окружности показан на рисунке.

Последний раз редактировалось Hottabych 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Турнир
Задача №7.
Было получено 2 решения.
Решения идентичные, в конечном итоге оба автора пришли к равенству , однако в решении №2 не т доказательства что не может быть
, однако в решении №2 не т доказательства что не может быть 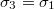 (что кстати может выполняться при отрицательных значениях x,y,z)
(что кстати может выполняться при отрицательных значениях x,y,z)
Поэтому за первое решение я поставил 5 баллов, за второе - 4 балла.
Было получено 2 решения.
1)
Обозначим. Заметим, что
. Тогда
. Аналогично
.
Условиебудет эквивалентно условию
.
После приведения подобных получим.
Используя стандартные обозначения для симметрических многочленов, последнее равенство перепишем в виде
.
Приводя подобные, получим
При условии (*) имеет место неравенство. Следовательно, получаем, что
.
2)
Найдем обратную функцию, функции f(x) и подставим ee в.
После преобразований получим:
отсюда следует
Решения идентичные, в конечном итоге оба автора пришли к равенству
Поэтому за первое решение я поставил 5 баллов, за второе - 4 балла.
Последний раз редактировалось a_l_e_x86 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Турнир
[quote name='a_l_e_x' date='20.8.2008, 15:53' post='42335']
Задача №7.
Было получено 2 решения.
[quote]
A какое авторское решение подразумевалось? условие намекает на тригонометрическую замену.
Задача №7.
Было получено 2 решения.
[quote]
A какое авторское решение подразумевалось? условие намекает на тригонометрическую замену.
Последний раз редактировалось Hottabych 29 ноя 2019, 19:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость