Решить иррациональное уравнение.
Добавлено: 31 дек 2013, 10:26
Дано уравнение:

где a - параметр. Требуется его решить приближенно. (точность? какая получится)
Можно сразу найти одно решение: при a=6 x=0
Было бы неразумно возводить это уравнение трижды в квадрат. Четыре радикала не помеха.
любой из них всегда можно убрать, например сделать подстановку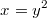 , но получим мы
, но получим мы
уравнение восьмой степени, которое более громоздко, чем наше. Попробуем решить это уравнение
по частям. Разложим его в ряд Тейлора, оставляя только x а первой степени. Имеем:

или

это простое квадратное уравнение относительно , решая его получим
, решая его получим
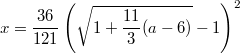
пошли дальше.
Попробуем получить теперь асимптотическое решение этого уравнения
Заменяя все радикалы на меньший ( ) получим неравенство
) получим неравенство
 или
или 
аналогично можно получить и второе неравенство
 или
или 
Итак мы имеем двойное неравенство

из этого неравенства следует решение

где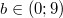
можно попробовать взять b=2,25, чтобы привязать решение к нашему уравнению
ведь при a=6 x=0. Можно. Но это не самое лучшее решение. Элементарный расчет
показывает, что лучше взять b=3,3.
то есть решение выглядит так

в этой формуле относительная погрешность при a>14 составляет всего 0,4%. Мало того
погрешность уменьшается пропорционально квадрату параметра a!! (фантастика!)
остался еще небольшой кусок (интервал) где решение ещё не найдено, полагаю, что это
не проблема. Надо рассмотреть функцию x=x(a). Это возрастающая вогнутая без каких-либо
особенностей функция. Возьмите ее три точки и решение практически в ваших руках
(ряд Тейлора применять не советую - замучают производные)
где a - параметр. Требуется его решить приближенно. (точность? какая получится)
Можно сразу найти одно решение: при a=6 x=0
Было бы неразумно возводить это уравнение трижды в квадрат. Четыре радикала не помеха.
любой из них всегда можно убрать, например сделать подстановку
уравнение восьмой степени, которое более громоздко, чем наше. Попробуем решить это уравнение
по частям. Разложим его в ряд Тейлора, оставляя только x а первой степени. Имеем:
или
это простое квадратное уравнение относительно
пошли дальше.
Попробуем получить теперь асимптотическое решение этого уравнения
Заменяя все радикалы на меньший (
аналогично можно получить и второе неравенство
Итак мы имеем двойное неравенство
из этого неравенства следует решение
где
можно попробовать взять b=2,25, чтобы привязать решение к нашему уравнению
ведь при a=6 x=0. Можно. Но это не самое лучшее решение. Элементарный расчет
показывает, что лучше взять b=3,3.
то есть решение выглядит так
в этой формуле относительная погрешность при a>14 составляет всего 0,4%. Мало того
погрешность уменьшается пропорционально квадрату параметра a!! (фантастика!)
остался еще небольшой кусок (интервал) где решение ещё не найдено, полагаю, что это
не проблема. Надо рассмотреть функцию x=x(a). Это возрастающая вогнутая без каких-либо
особенностей функция. Возьмите ее три точки и решение практически в ваших руках
(ряд Тейлора применять не советую - замучают производные)