Страница 1 из 3
Как получать большие простые числа?
Добавлено: 12 авг 2014, 06:38
Alexu007
Г-жа omega в соседней теме мутит с большим количеством не очень больших случайных чисел. Хотелось бы информации, как их всё-таки добывать - быстро и в больших количествах?
Например: я написал программу, которая ищет эти простые числа "почти тупым делением". Максимальное простое число, умещающееся в uint_64 равно 18446744073709551557 - т.е. 20 разрядов. Это число вычисляется приблизительно за полторы минуты - что убивает возможность массового получения даже таких относительно небольших чисел.
Решето Эрастофена, Аткина требуют памяти. 4 гига памяти моего ноутбука (которая наполовину занята системой) это всего 4 * 10^9 байт - как то интуиция подсказывает, что этого маловато для чисел размером 10^20. И забить весь жёсткий диск в терабайт - это только 10^12 байт плюс катастрофическое падение скорости.
Какие ещё варианты быстрого нахождения подобных чисел?
Как получать большие простые числа?
Добавлено: 12 авг 2014, 07:31
zykov
На википедии есть статья про это:
Primality test.
Это на английском. Версия на русском там совсем убогая (просто список разных методов).
Как получать большие простые числа?
Добавлено: 12 авг 2014, 08:19
Дмитрий40
Решетом они ищутся. Эрастофена или другим (Сундарама или Аткина).
Памяти надо, да. Для чисел до 2^64 (до 1.8*10^19) памяти надо примерно 800МБ. Можно или ускорить вычисления затребовав где-то вдвое-втрое больше памяти, или наоборот ужать требования по памяти, замедлив расчёты.
Объём памяти считается несложно, можно даже без интуиции, 32 бита умножить на 204 миллиона - простых чисел до 2^32 - их достаточно для проверки всех чисел вплоть до 2^64. Т.е. память нужна лишь для хранения простых чисел до sqrt(проверяемое число).
Делениями искать такие числа ОЧЕНЬ долго, это применимо лишь для чисел до нескольких тысяч, дальше любое решето сильно быстрее. Хотя даже деления должны выполняться быстрее, ведь для проверки одного числа достаточно выполнить ~200млн делений, это буквально секунды.
Как получать большие простые числа?
Добавлено: 12 авг 2014, 08:22
Sonic86
В худшем случае - решетом, но есть и другие, более быстрые методы.
Кстати, формулы пишите в

.
которые являются ссылками на другие статьи Википедии. Так что легким движением руки список превращается...
Василенко Теоретико-числовые методы в криптографии - почитайте, там есть способы.
Самый простой нетривиальный тест - тест простоты Люка. (
ссыль на русскую вику)
(сразу следует заметить, что если Вам нужны длинные списки последовательных простых чисел, то это - другой вопрос)
Как получать большие простые числа?
Добавлено: 12 авг 2014, 08:40
Дмитрий40
Не соглашусь. Решето удобно для получения именно большого количества гарантированно простых чисел. И в такой задаче альтернатив им не просматривается. Для отдельных чисел есть и другие более быстрые способы, да. Но вопрос был именно про много чисел.
Как получать большие простые числа?
Добавлено: 12 авг 2014, 11:26
Sonic86
Дмитрий40 писал(а):Source of the post Не соглашусь. Решето удобно для получения именно большого количества гарантированно простых чисел. И в такой задаче альтернатив им не просматривается. Для отдельных чисел есть и другие более быстрые способы, да. Но вопрос был именно про много чисел.
AKS-тест работает за

. Для проверки
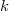
подряд идущих чисел длины

достаточно

операций.
Решето проверяет
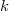
подряд идущих чисел за

операций.
Вот и думайте, что Вам лучше. :huh:
(привести оценку памяти затрудняюсь)
Как получать большие простые числа?
Добавлено: 12 авг 2014, 11:55
folk
Для решета оценка по моему неверная. Для Аткина видел оценку
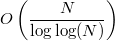
для поиска простых в диапазоне [N,N+k] надо потратить

Для N порядка 10^20 числа под О таковы, что для Аткина оно меньше чем для
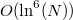
Как получать большие простые числа?
Добавлено: 12 авг 2014, 12:23
Alexu007
Дмитрий40 писал(а):Source of the post Объём памяти считается несложно, можно даже без интуиции, 32 бита умножить на 204 миллиона - простых чисел до 2^32 - их достаточно для проверки всех чисел вплоть до 2^64. Т.е. память нужна лишь для хранения простых чисел до sqrt(проверяемое число).
В решете же хранятся все числа, и простые и составные. Только там на позиции простых чисел 1, а составных - 0 (или наоборот). Так что памяти всё же надо
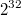
байт - чтобы работало боле-мене быстро (заморачивание с битами и тем более с делением памяти на "37" ИМХО сильно уменьшит быстродействие).
Но и это только для чисел размером до
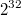
байт. Далее ими можно воспользоваться для деления чисел до
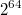
(и тогда достаточно этих простых чисел), либо продолжать решето с соответствующим расходом памяти. Или я не прав?
Как получать большие простые числа?
Добавлено: 12 авг 2014, 13:25
Gassa
Sonic86 писал(а):Source of the post AKS-тест работает за

. Для проверки
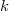
подряд идущих чисел длины

достаточно

операций.
Решето проверяет
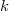
подряд идущих чисел за

операций.
Вот и думайте, что Вам лучше. :huh:
(привести оценку памяти затрудняюсь)
А что, AKS-тест реально применяется? Я думал, это чисто теоретический результат, и константа там такая, что для любых разумных задач существуют более практичные методы. Для маленьких - простая проверка на простоту делением. Если надо много маленьких - решето. Если надо большие - вероятностная проверка тестом Миллера-Рабина.
Как получать большие простые числа?
Добавлено: 12 авг 2014, 13:43
folk
Alexu007 писал(а):Source of the post Далее ими можно воспользоваться для деления чисел до
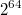
(и тогда достаточно этих простых чисел), либо продолжать решето с соответствующим расходом памяти. Или я не прав?
Насколько я понял в primesieve все же хранятся побитово - выигрыш за счет L2 кэша больше чем экономия на битовых операциях. Также там вроде как не хранятся делящиеся на 2,3,5. (информация не стопроцентная - читал про нее в инете просто)
У меня эта программа сломалась на 5*10^18 при памяти в ноуте 2Gb.