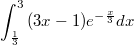Страница 1 из 3
Интегрирование по частям
Добавлено: 28 мар 2013, 21:25
Alexander4321
Добрый день! Необходимо вычислить определенный интреграл
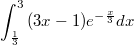
Интегрирую по частям. Но чем дальше интегрирую, тем меньше не становится. Извиняюсь что не пишу расчет в тексте, прикрепил файл Word (в нем уже записаны все произведенные расчеты, столько в тексте не выдержу писать). Можете посмотреть, может я не тот метод выбрал для интегрирования? Спасибо!

Интегрирование по частям
Добавлено: 29 мар 2013, 03:02
bot

Дальше сами.
Интегрирование по частям
Добавлено: 29 мар 2013, 08:26
Alexander4321
Можете пояснить, как

в
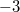
преобразовался? Спасибо!
Интегрирование по частям
Добавлено: 29 мар 2013, 10:34
laplas
вы правило интегрирования по частям знаете?
если нет, то знаете ли вы правило дифференцирования произведения двух функций?
если и это не знаете, тогда вас отправят учебник читать!
Интегрирование по частям
Добавлено: 29 мар 2013, 11:32
Alexander4321
Не надо, я сам. Вечером почитаю по учебнику, попробую разобраться.
Интегрирование по частям
Добавлено: 30 мар 2013, 20:58
Alexander4321
При интегрировании по частям что-то вроде этого получается


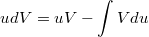

А как получилось
понятия не имею.
Интегрирование по частям
Добавлено: 30 мар 2013, 21:25
Dragon27
Последнее неверно.
Вы знаете, что такое "дифференциал"? Вы ж сами выше писали.

, где

- производная
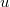
по

. Отсюда можно заметить, что

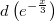
- это дифференциал от
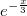

Интегрирование по частям
Добавлено: 30 мар 2013, 21:25
vetrjanka

Учите свойства интегралов.
Интегрирование по частям
Добавлено: 31 мар 2013, 06:01
Alexander4321
Точно, тут же получается

Спасибо!
Интегрирование по частям
Добавлено: 31 мар 2013, 17:19
Alexander4321
Дошло наконец, как чисто технически были выполнены преобразования.

Но вот почему мы под знаком интеграла трогали только
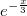
и проигнорировали
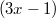
все равно не понятно. Можете скинуть какую-нибудь ссылку на ресурс или назвать конкретную тему из учебника (что-нибудь конкретное, а не весь раздел), что можно почитать, чтобы разобраться? Пока это не пойму, даже не хочется дальше разбираться с заданием. Спасибо!