тервер
Добавлено: 28 сен 2011, 17:41
Все-таки почему  ?
?
С одной стороны,
И тогда получается, что

Однако не все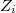 независимы, а независим будет набор из не более чем
независимы, а независим будет набор из не более чем 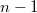 таких случайных величин, и это, как я понимаю, и есть причина того, что в
таких случайных величин, и это, как я понимаю, и есть причина того, что в  именно
именно 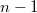 степень свободы. Но логику все равно не до конца улавливаю. Возьмем, мы скажем, в этой сумме и выделим
степень свободы. Но логику все равно не до конца улавливаю. Возьмем, мы скажем, в этой сумме и выделим 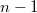 слагаемых
слагаемых  , и получившееся выражение и будет распределено так (т.к. все сл.в. независимы), согласен, но кто сказал что распределение сохранится, если мы добавим в сумму
, и получившееся выражение и будет распределено так (т.к. все сл.в. независимы), согласен, но кто сказал что распределение сохранится, если мы добавим в сумму 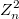 ?
?
С одной стороны,
И тогда получается, что
Однако не все