yourdomain.com

Нужно доказать, что выражение 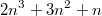без остатка делится на 6 при любом целом

Насколько я знаю, число делится на 6, когда оно делится одновременно на 2, и на 3. Ну, насчет того, что число четное, вопросов нет, но вот о делении на 3... Число делится на три, когда сумма его цифр делится на три, но в этом случае этот признак никак не может нам помочь, ведь само число мы точно не знаем. Тогда получается, что выражение нужно разложить на множители и чтобы каждый из них делился на 3. В этом и есть основная проблема, никак не пойму как это сделать. Заранее спасибо

Доказательство по индукции. Никаких признаков делимости здесь не надо.

Спасибо, через сутки мучений решение нашлось, как подсказывал Andrew58

Помогите еще с одной задачкой. Думаю, половину я решил, а вот дальше.. Нужно найти все целые значения , при которых число является простым. Решение, вроде бы, всего одно: . Также понятно, что n - нечетное число. А вот как доказать, что решение всего одно, непонятно :blink: Объясните пожалуйста

Ну если должно быть целым, а не обязательно натуральным, то подходит еще и (как минимум, может еще что-то проглядел).
А решение примерно такое. Т.к. и всегда разной четности, а их произведение делится на 4, то одно из этих чисел делится на 4. При этом либо оно равно 4 (или -4, если все-таки допускаются отрицательные значения), либо другое число равно 1 (или -1), иначе простого числа не получится. Получается не так много вариантов, которые можно проверить перебором. Не знаю только, что делать с такими случаями, как , где получается число - считать его простым или нет, потому что обычно простыми называют только натуральные числа, а тут дано как целое... здесь не очень понятно.

Да, действительно немного странно, что n именно целое, а не натуральное, но в условии написано именно так. Я решил, что пусть n может быть отрицательным целым, но полученное число должно получиться исключительно простым положительным числом. Не знаю, могут ли отрицательные числа быть простыми, но предположу, что нет. Может кто исправит меня

В итоге у меня получилось три решения:

Traim писал(а):Source of the post

Тогда и тоже.