Колебания
Добавлено: 08 сен 2010, 17:48
Амплитуда колебаний материальной точки A=1 см, частота 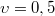 Гц. Запишите кинематический закон движения x(t) и постройте график зависимости координаты точки от времени. Определите фазу
Гц. Запишите кинематический закон движения x(t) и постройте график зависимости координаты точки от времени. Определите фазу 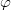 и координату х точки через промежуток времени
и координату х точки через промежуток времени c. Считайте, что в начальный момент времени х=0 начальная фаза
c. Считайте, что в начальный момент времени х=0 начальная фаза 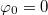 .
.
Помогиет пожалуйста , a то я в этих колебания пока что ничего не могу понять .
Помогиет пожалуйста , a то я в этих колебания пока что ничего не могу понять .