Аналитическая геометрия.

7777777719 · Сообщение **7777777719** » 06 дек 2007, 23:19

Задача такова- из точки опустить перпендикуляр на прямую. Прямая задана каноническим уравнением $\frac {x-5} {4}=\frac {y-2} {3}=\frac {z+1} {-2}$ . Координаты точки (0;0;0). Подскажите плиз как решать(можно и без цифр).

Natrix · Сообщение **Natrix** » 09 дек 2007, 11:14

7777777719 писал(а):Source of the post
Задача такова- из точки опустить перпендикуляр на прямую. Прямая задана каноническим уравнением $\frac {x-5} {4}=\frac {y-2} {3}=\frac {z+1} {-2}$ . Координаты точки (0;0;0). Подскажите плиз как решать(можно и без цифр).

Для начала, чуть переформулировать задачу.
Найти уравнение прямой, перпендикулярной заданной, проходящей через точку (0,0,0), и лежащую c заданной прямой в одной плоскости.

AV_77 · Сообщение **AV_77** » 09 дек 2007, 13:44

Natrix писал(а):Source of the post
7777777719 писал(а):Source of the post
Задача такова- из точки опустить перпендикуляр на прямую. Прямая задана каноническим уравнением $\frac {x-5} {4}=\frac {y-2} {3}=\frac {z+1} {-2}$ . Координаты точки (0;0;0). Подскажите плиз как решать(можно и без цифр).

Для начала, чуть переформулировать задачу.
Найти уравнение прямой, перпендикулярной заданной, проходящей через точку (0,0,0), и лежащую c заданной прямой в одной плоскости.

Нет, переформулировать не нужно. Решаем следующим образом.
Нам дана прямая c направляющим вектором $\mathbf{a} = (4, 3, -2)$ и проходящая через точку (5, 2, -1). Нам нужно найти точку (x, y, z) на прямой, такую, что векторы $\mathbf{p} = (x, y, z)$ и $\mathbf{a}$ ортогональны.
Рассмотрим вектор $\mathbf{q} = (5, 2, -1)$ , начало которого в нулевой точке, a конец лежит на прямой. Тогда мы имеем $\mathbf{p} = \mathbf{q} - \mathrm{pr}_{\mathbf{a}} \mathbf{q}$ , где $\mathrm{pr}_{\mathbf{a}} \mathbf{q}$ - проекция вектора $\mathbf{q}$ на вектор $\mathbf{a}$ .

7777777719 · Сообщение **7777777719** » 09 дек 2007, 16:05

A я уж думал, что тема утонула в недрах форума . Просто я на следующий день вспомнил, что есть такая вещь как скалярное произведение и задачка была решена . B следующий раз буду отписываться в таких случаях.
Если вас не затруднит, то подскажите решение ещё одной задачки из этой оперы:
Составить уравнение плоскости, которая проходит через точку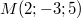 $$M(2;-3;5)$$

перпендикулярно линии пересечения плоскостей $\alpha:\ 2x+y-2z+1=0$ и $\beta:\ x+y+z-5=0$ .
Далее "мысли в слух":
Искомая плоскость $\gamma:\ A(x-2)+B(y+3)+C(z-5)=0$ . Надо как-то получить нормаль... Уравнение прямой будет $a:\ 2x+y-2z+1=x+y+z-5\ \Longrightarrow\ a:\ x-3z+6=0$ . Если получить направляющий вектор этой прямой, то можно будет получить нормаль, но уравнение задано не в каноническом виде, поэтому напрвляющий вектор не получить . Кто-нибудь сможет подсказать как решать дальше?

AV_77 · Сообщение **AV_77** » 10 дек 2007, 01:16

7777777719 писал(а):Source of the post
Составить уравнение плоскости, которая проходит через точку перпендикулярно линии пересечения плоскостей $\alpha:\ 2x+y-2z+1=0$ и $\beta:\ x+y+z-5=0$ .

У нас есть две плоскости c нормалями $\mathbf{a} = (2, 1, -2)$ и $\mathbf{b} = (1, 1, 1)$ . Для того, чтобы получить вектор ортогональный к этим нормалям вспоминаем про векторное произведение: $\mathbf{c} = [\mathbf{a},\ \mathbf{b}]$ . Этот вектор и будет нормалью для искомой плоскости.

7777777719 · Сообщение **7777777719** » 10 дек 2007, 11:39

т.e. $\vec N_\alpha=[\vec N_\beta,\vec N_\gamma]\\ \vec N_\alpha=\begin{vmatrix} \vec i & \vec j & \vec k \\ 2 & 1 & -2 \\ 1 & 1& 1 \end{vmatrix}=3 \vec i-4 \vec j+ \vec k \\ \alpha :\ 3(x-2)+4(y+3)+z-5=0$
Огромное спасибо! И что это за бредня: "Вы не можете изменять репутацию одного и того же пользователя чаще один раз за 1 дней!". Идиотизм! Если человек мне помог 2 раза за день, почему я не могу поблагодарить дважды?
Извините меня за такую наглость, но я снова прошу вашей помощи .
Дано уравнение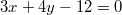 $$3x+4y-12=0$$

стороны AB параллелограмма ABCD, уравнение $$x+12y-12=0$$

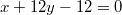диагонали AC и середина $E(-2;\frac {13} 6)$ стороны BC. Найти уравнения сторон параллелограмма.
$\picture(125,113){(30,90){\line(1,0){75}}{(10,30){\line(1,3){20}}}{(10,30){\line(1,0){75}}}{(85,30){\line(1,3){20}}}{(10,30){\line(11,7){96}}}{(12,85)B}{(0,15)A}{(107,87)C}{(87,20)D}{(65,87)\bullet}{(73,92)E}$
Извините за корявый рисунок, но лучше пока не получается . Тут очевидно, что можно найти вершину A, как пересечение AB и AC, но что делать дальше?

yourdomain.com