yourdomain.com

Anik писал(а):Source of the post
Выражение для $R_1(t)=R\sqrt{1-\sin^2(\omega t)sin^2\alpha}$ уже нашёл.
Нашёл, также, зависимость линейной скорости точки от времени:
$v_1(t)=R\omega t\sqrt{1-cos^2(\omega t)\sin^2\alpha}$ .
Здесь ошибка, должно быть так:
$v_1(t)=R\omega\sqrt{1-cos^2(\omega t)\sin^2\alpha}$ .

Теперь, нашёл выражение для $\dot\varphi (t)$
$\dot\varphi (t)=\frac{H_1}{m_1R^2(1-\sin^2\alpha\sin^2\omega t)}$
Подстановка выражений для $$R_1(t)$$

и $\dot\varphi (t)$ в первое дифференциальное уравнение:
$2\dot R_1\dot\varphi+R_1\ddot\varphi=0$ , обращает его в тождество. (Нужно иметь в виду, что $\sin\alpha - const$ ).
Теперь, подставлю эти значения во второе дифференциальное уравнение:
$m_1\ddot R_1-m_1R_1\dot\varphi^2=\frac{k(m_1+m_2)}{m_2}R_1$ ,
посмотрю, что получится.

Anik писал(а):Source of the post
Подстановка выражений для и $\dot\varphi (t)$ в первое дифференциальное уравнение:
$2\dot R_1\dot\varphi+R_1\ddot\varphi=0$ , обращает его в тождество. (Нужно иметь в виду, что $\sin\alpha - const$ ).

Не поверю, пока не приведете выкладки. Даже не все, а хотя бы явное выражение для $\ddot\varphi$ .

grigoriy писал(а):Source of the post
Anik писал(а):Source of the post
Подстановка выражений для и $\dot\varphi (t)$ в первое дифференциальное уравнение:
$2\dot R_1\dot\varphi+R_1\ddot\varphi=0$ , обращает его в тождество. (Нужно иметь в виду, что $\sin\alpha - const$ ).

Не поверю, пока не приведете выкладки. Даже не все, а хотя бы явное выражение для $\ddot\varphi$ .

$\ddot\varphi =\frac{2H_1\omega \sin^2\alpha\sin\omega t\cos\omega t}{m_1R^2(1-\sin^2\alpha\sin^2\omega t)^2}$

Anik писал(а):Source of the post
$\ddot\varphi =\frac{2H_1\omega \sin^2\alpha\sin\omega t\cos\omega t}{m_1R^2(1-\sin^2\alpha\sin^2\omega t)^2}$

Кажется, минус потеряли. Там он выскакивает трижды.
А на это так и не ответили.

grigoriy писал(а):Source of the post
Т.е. - это модуль полной скорости, а не её проекция на ?
Да, и как лепить к конструкции "2 шарика+пружинка" угол $\alpha$ ?

Извиняюсь, соврал насчет минуса. Выскакивает дважды. Все верно.
Но пока вы не сорвете маску с таинственной личности $\alpha$ ,
разбираться в ваших построения особого желания нет.

grigoriy писал(а):Source of the post
Anik писал(а):Source of the post
$\ddot\varphi =\frac{2H_1\omega \sin^2\alpha\sin\omega t\cos\omega t}{m_1R^2(1-\sin^2\alpha\sin^2\omega t)^2}$

Кажется, минус потеряли. Там он выскакивает трижды.
А на это так и не ответили.
grigoriy писал(а):Source of the post
Т.е. - это модуль полной скорости, а не её проекция на ?
Да, и как лепить к конструкции "2 шарика+пружинка" угол $\alpha$ ?

Никакой минус я там не терял.
$$v_1$$

это модуль линейной скорости движения точки $$m_1$$

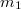
по эллипсу.
Конструкцию "2 шарика+пружинка" я привёл к движению одного шарика+пружинка с эквивалентной жёсткостью. А угол $\alpha$ это угол между плоскостью, в которой по кругу равномерно вращается изображающая точка (радиус R), и плоскостью в которой по эллипсу движется реальная точка $$m_1$$

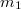
. Изображающая окружность проецируется на плоскость движения точки $$m_1$$

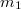
под углом $\alpha$ и получается эллипс, как траектория движения точки $$m_1$$

.
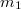
***См. рисунок, который я трижды приводил, это хорошая геометрическая интерпретация движения точки $$m_1$$

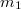
по эллипсу, как проекции кругового движения изображающей точки, которая равномерно вращается по окружности с радиусом $$R$$

.
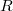
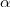
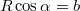
***Можете считать, что угол $\alpha$ задан начальными условиями движения. А вообще, $R\cos\alpha=b$ , где $b$

малая полуось эллипса, а $R$

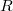
- большая полуось эллипса.

Anik писал(а):Source of the post
Изображающая окружность проецируется на плоскость движения точки под углом $\alpha$ и получается эллипс, как траектория движения точки .

Ага, не меняя начальных условий, просто посмотрели под другим углом зрения.
Я вот возьму, например, и посмотрю на круговую орбиту спутника под другим углом.
И увижу эллипс со всеми законами Кеплера.

grigoriy писал(а):Source of the post Я вот возьму, например, и посмотрю на круговую орбиту спутника под другим углом.
И увижу эллипс со всеми законами Кеплера. B)

Не получится. Центр Земли не будет в центре эллипса.

grigoriy писал(а):Source of the post
Anik писал(а):Source of the post
Изображающая окружность проецируется на плоскость движения точки под углом $\alpha$ и получается эллипс, как траектория движения точки .

Ага, не меняя начальных условий, просто посмотрели под другим углом зрения.
Я вот возьму, например, и посмотрю на круговую орбиту спутника под другим углом.
И увижу эллипс со всеми законами Кеплера.

Нет, здесь уже так не будет.
Дело в том, что спутник вращается притягиваясь к центру по закону обратных квадратов, и этот центр будет в фокусе эллипса.
Если вы посмотрите на круговую орбиту спутника под углом, то увидите, что спутник вращается по эллипсу так, что центр вращения находится в центре эллипса, а это не будет соответствовать ЗВТ.

Anik писал(а):Source of the post ***Можете считать, что угол $\alpha$ задан начальными условиями движения.

Нет, всё-таки, так считать нельзя: начальные условия заданы и в них угла альфа нет.

Рубен писал(а):Source of the post
Anik писал(а):Source of the post ***Можете считать, что угол $\alpha$ задан начальными условиями движения.
Нет, всё-таки, так считать нельзя: начальные условия заданы и в них угла альфа нет.

Но я же раньше писал, что угол $\alpha$ можно потом выразить через "более естественные" начальные условия.

yourdomain.com

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику