yourdomain.com

Итак, в первом "школьном" решении радиус-вектор точки изменялся только по направлению, равномерно вращаясь, а во втором "школьном" решении радиус-вектор точки изменялся только по модулю, и точка колебалась вдоль прямой. В общем случае радиус-вектор будет изменяться и по модулю и по направлению.
Докажем, что в общем случае каждая точка будет двигаться по эллипсу так, что ц.м. системы двух точек будет в центре эллипса.
Заметим, что при таком движении за один период поворота радиус-вектора вокруг ц.м. модуль радиус-вектора дважды достигнет максимальной (и минимальной) длины. Это значит, что модуль будет изменяться с двойной частотой по отношению к частоте обращения вокруг ц.м.

Эксцентриситет эллипса будет зависеть от угла $\alpha$ . Предположим, сначала, что угол $\alpha$ задан начальными условиями движения, потом этот угол будет выражен через "более естественные" начальные условия (сейчас пока трудно сказать, какие именно). В процессе движения этот угол остаётся постоянным
Теперь, нам нужно связать геометрические параметры вращения вектора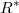 $$R^*$$

по кругу с параметрами вращения вектора $\displaystyle \blue R_1$ по эллипсу. Если бы мы знали как изменяется угол между векторами $$R^*$$

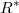и

, в зависимости от углов $\varphi^*$ и $\alpha$ , то нашли бы и связь между модулями векторов $$R^*$$

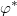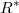и

, поскольку вектор $$R_1$$

есть проекция вектора $$R^*$$

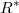на горизонтальную плоскость.

На рисунке, изображающая точка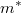 $$m^*$$

движется равномерно по дуге большого круга проходящей через точки $$A,m^*,C$$

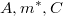, а действительная точка $$m_1$$

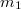движется по дуге эллипса (изображён синим цветом), который лежит в горизонтальной плоскости (круг с дугой $$A,c,B$$

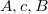). Угол между плоскостью движения изображающей точки и горизонтальной плоскостью (в которой эллипс) обозначен как $\alpha$ . Заметим, что $$A$$

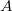это и есть двугранный угол $\alpha$ , поскольку угол $$C$$

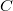(тоже двугранный) прямой.
Угол между векторами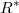 $$R^*$$

и

на рисунке обозначен буквой $$x$$

. Этот угол можно найти из сферического треугольника со сторонами $\varphi ^*,\varphi$ и $$x$$

.

Пока хватит, остальное - завтра.
***Устранил ошибку, везде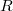 $$R$$

поправил на $$R_1$$

.

Anik писал(а):Source of the post Это значит, что модуль будет изменяться с двойной частотой по отношению к частоте обращения вокруг ц.м.

Это заведомо неверно. Посмотрите на график радиуса эллипса $r(\phi)$ как функции угла. Эта функция периодическая с периодом $\phi_0=2\pi$ - как раз период обращения. Если учесть, что угол и частота равномерного вращения связана параметром t: $\phi = \omega t$ , то равенство периодов влечет равенство циклических частот.

Остальное даже не читал.

Рубен писал(а):Source of the post
Anik писал(а):Source of the post Это значит, что модуль будет изменяться с двойной частотой по отношению к частоте обращения вокруг ц.м.

Это заведомо неверно. Посмотрите на график радиуса эллипса $r(\phi)$ как функции угла. Эта функция периодическая с периодом $\phi_0=2\pi$ - как раз период обращения. Если учесть, что угол и частота равномерного вращения связана параметром t: $\phi = \omega t$ , то равенство периодов влечет равенство циклических частот.

Остальное даже не читал.

Я не знаю, что у вас за графики. Возможно там радиус-векторы проведены из фокуса эллипса, тогда периоды совпадают. Но, это случай взаимодействия по закону обратных квадратов.
В нашем случае, радиус-векторы проведены из центра эллипса, вот здесь получается двойная частота для модуля радиус-вектора.
Да это же очевидно, за один оборот радиус-вектора он дважды побывает в афелии и перигелии. Максимальное значение модуля равно большой полуоси эллипса, а минимальное значение модуля радиус-вектора равно малой полуоси эллипса. Вот поверните этот радиус-вектор на один оборот и сами убедитесь.

Ок.

Вот, когда я писал, что движение точки по кругу под действием восстанавливающей силы из центра, следует из механических соображений, вы написали, что это пурга. Колебательное движение вдоль одной прямой, тоже следует и соображений механики.
Сейчас я поясню, что это за соображения.
Вы согласны с тем, что малые колебания математического маятника можно приближённо рассматривать как движение массы под действием центральной силы, пропорциональной отклонению маятника? Это приближение настолько точно, насколько можно считать синус малого угла равным самому углу.

Так вот, такой маятник может колебаться вдоль прямой, совершать движение по окружности, или двигаться по эллипсу, центр которого в центре равновесия.
Подвесьте гаечку на ниточке к потолку и толкните её. Вы сами увидите, что такие движения гаечки возможны.

Anik писал(а):Source of the post Вот, когда я писал, что движение точки по кругу под действием восстанавливающей силы из центра, следует из механических соображений, вы написали, что это пурга.

Пурга - это решение уравнений движения "из механических соображений".

В любом случае, точка не будет двигаться по эллипсу, т.к. колебания её радиуса будет определяться далеко не только частотой вращения и находиться не по формуле $2\omega$ . Вообщем, это всё лирика. Когда будет решение, мы его просто подставим в исходное уравнение. Если оно ему удовлетворит, то всё ок. Если нет - значит оно неверное.

Ок.

Было:

$\displaystyle r^2=\frac{r_0^2}{2}\left[ \left(1-\frac{\mu\omega_0^2}{k}\right)\cos2\sqrt{\frac{k}{\mu}}t+1+\frac{\mu\omega_0^2}{k} \right]$

Для угла:

$\displaystyle \varphi=\arctg\left(\omega_0\sqrt{\frac{\mu}{k}}\tg\sqrt{\frac{k}{\mu}}t\right)$

После исключения $$t$$

- уравнение траектории:

$\displaystyle r^2=\frac{r_0^2}{2}\left[ \left(1-\frac{\mu\omega_0^2}{k}\right)\frac{\cos^2\varphi-\frac{k}{\omega_0^2\mu}\sin^2\varphi}{\cos^2\varphi+\frac{k}{\omega_0^2\mu}\sin^2\varphi}+1+\frac{\mu\omega_0^2}{k} \right]$

С какого бодуна тут можно унюхать эллипс...

Гришпута, покажииииите ЕЁ !

Рубен писал(а):Source of the post
Гришпута, покажииииите ЕЁ !

Рубен, на сегодня я сдулся! Как-нибудь на днях.

yourdomain.com

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику

Анику про механику