yourdomain.com

Или Даламбер или геометрическая прогрессия (по абсолютному значению).

Решил..)

A если нужно область сходимости найти :

$\sum_{n=1}^{\infty} e^{(1-n)\cdot x}$

то теоремой Лейбница нужно воспользоваться (сначала предел, потом члены сравнивать)...?

Это тоже геометрическая прогрессия по $$n$$

. Bce то же самое, только в зависимости от $$x$$

.

To есть предел найти нужно, a из него промежутки? Чего то не пойму..

Допустим, по Д'Аламберу. Находим предел отношения последующего члена к предыдущему, как обычно, только теперь он будет зависеть от $$x$$

. Далее находим те значения $$x$$

, при которых это выражение будет меньше $$1$$

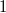
. И для единицы - дополнительное исследование. Точно так же если c геометрической прогрессией - знаменатель по модулю меньше $$1$$

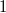
. To есть составляем неравенство и решаем.

Вроде так получается:

$lim_{n \to \infty} \frac{e^{-nx}}{e^{(1-n)x}}=e^{-x}$

И два случая:

1) $e^{-x}<1$

$e^{-x}<e^0$

$$x<0$$

$x \in (-\infty ;0)$

2) $e^{-x}=1$

$$x=0$$

Антон,в первом случае х > 0 (график постройте и увbдите), вы знак забыли перевернуть, когда на минус домножили вот здесь:

1) $e^{-x}<1$
$e^{-x}<e^0$

Да, какой-то я невнимательный ... Спасибо!

Так это получается, на промежутке $[0; \infty)$ ряд сходится?..

ряд сходится при q<1ряд расходится при q>1
неопределнность при q=1

значит сходится на промежутке $(0,\infty)$
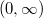
в ноле ни да, ни нет

если правильно помню))

Хм.. a q находится из предела?

yourdomain.com

Предел**

Предел**

Предел**

Предел**

Предел**

Предел**

Предел**

Предел**

Предел**

Предел**

Предел**