Шарик на плоскости

Ответить на сообщение
Аватар пользователя
ALEX165
Сообщений: 10578
Зарегистрирован: 30 сен 2008, 21:00

Шарик на плоскости

Сообщение ALEX165 » 18 янв 2013, 10:36

На проводящей плоскости лежит проводящий шарик радиуса R. Всё это находится во внешнем постоянном, пространственно однородном электрическом поле E, направленном перпендикулярно плоскости. Шарик отрывают от плоскости. Вопрос - какой заряд унесёт шарик (какой суммарный заряд будет на шарике после отрыва)?
Изображение

Я решаю так.
Принимаю потенциал плоскости за 0, начало координат в центре шарика до отрыва, ось z - перпендикулярно плоскости вверх, задаюсь плотностью поверхностного заряда на шарике $$\sigma(z)$$, рисую зеркальный шарик - отражение исходного под плоскостью, задаюсь плотностью заряда на нём $$-\sigma(z)$$, вычисляю потенциал точки кольца, параллельного плоскости, на поверхности шарика с координатой z как сумму потенциалов, создаваеммых всем шариком, зеркальным шариком и внешним полем и приравниваю его 0:
$$\varphi_{øàðèê}+\varphi_{çåðêàëüíûé}-(R+z)E=0$$,
откуда нахожу $$\sigma(z)$$, интегрирую её по всему шарику и получаю его заряд.

(По размерности это просто $$\epsilon \epsilon_0 ER^2$$, но что-то маловато).

Соответственно два вопроса.
1. Нет ли у меня ошибки?
2. Нет ли способа попроще это решить (вычисления сложноваСтенькие...) ?
Последний раз редактировалось ALEX165 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
lapay
Сообщений: 266
Зарегистрирован: 29 фев 2012, 21:00

Шарик на плоскости

Сообщение lapay » 18 янв 2013, 15:20

На вскидку, заряд шарика будет раза в два меньше, чем у свободного шарика, заряженного потенциалом $$U=ER$$. А вот точно посчитать сложновато будет.
Последний раз редактировалось lapay 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
peregoudov
Сообщений: 1917
Зарегистрирован: 09 сен 2007, 21:00

Шарик на плоскости

Сообщение peregoudov » 18 янв 2013, 17:23

ALEX165 писал(а):Source of the post откуда нахожу $$\sigma(z)$$,
Лихо! Там же вообще-то интегральное уравнение выходит. А в целом все правильно, вроде.

Я посмотрел аналогичную двумерную задачку. Там можно применить комплексный анализ и найти точное решение в конечном виде: если радиус шарика равен $$1/\pi$$, а плоскость расположена при $$\mathop{\rm Re}z=0$$, то потенциал $$\phi=\ctg\frac1z$$. Отсюда нетрудно выписать интеграл для заряда шарика. С интегралом неохота возиться, вроде он тоже вычисляется в конечном виде вычетами.

А для трехмерной задачки наиболее экономичным методом, наверное, будет последовательное применение метода изображений для сферы и плоскости и построение решения в виде поля бесконечного ряда точечных зарядов. Надо только придумать, как этот ряд начать

P. S. А, ну, вроде и придумывать особенно нечего: первый член --- диполь в центре шара. P. P. S. Не, вру, не диполь --- диполь плюс заряд. P. P. P. S. А дальше вообще красиво! Если вас интересует только заряд шара, диполи не важны, и можно ограничиться зарядами. Там простой ряд должен получиться... P. P. P. P. S. Что-то он у меня расходится...

Неплохая задачка. Сами придумали?
Последний раз редактировалось peregoudov 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
Аватар пользователя
ALEX165
Сообщений: 10578
Зарегистрирован: 30 сен 2008, 21:00

Шарик на плоскости

Сообщение ALEX165 » 18 янв 2013, 17:43

peregoudov писал(а):Source of the post
Неплохая задачка. Сами придумали?

Это из жизни, их там куча получается...
Последний раз редактировалось ALEX165 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
Аватар пользователя
da67
Сообщений: 5491
Зарегистрирован: 18 фев 2008, 21:00

Шарик на плоскости

Сообщение da67 » 19 янв 2013, 19:10

Инверсия относительно точки касания не поможет?
Последний раз редактировалось da67 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
peregoudov
Сообщений: 1917
Зарегистрирован: 09 сен 2007, 21:00

Шарик на плоскости

Сообщение peregoudov » 19 янв 2013, 20:22

Под катом --- более детально расписанное решение двумерной задачи.
Пусть плоскость находится при $$x=0$$, а труба описывается уравнением $$(x-1/\pi)^2+y^2=1/\pi^2$$. Уравнение Лапласа решается в области справа от плоскости и вне трубы. На бесконечности должно быть $$\phi=x+\ldots$$.

Поскольку граница области состоит из прямых и окружностей, то естественно попробовать упростить задачу, используя дробно-линейное преобразование. Возьмем $$w=1/z$$, тогда на плоскости $$w$$ область представляет собой полосу $$0<\mathop{\rm Re}w<\pi/2$$, а при $$w\to0$$ комплексный потенциал должен иметь вид $$\psi=1/w+\ldots$$. Используя принцип отображений для плоскости, находим

$$\displaystyle \psi=\sum_{n=-\infty}^\infty\frac1{w-\pi n}=\ctg w=\ctg\frac1z. $$

Вещественную часть (вещественный потенциал) можно записать в виде

$$\displaystyle \phi=\frac{\sin\frac{2x}{x^2+y^2}}{\ch\frac{2y}{x^2+y^2}-\cos\frac{2x}{x^2+y^2}}. $$

Чтобы вычислить заряд трубы, используем $$E_n=4\pi\sigma$$. Если касательный вектор к границе имеет вид $$(dx,dy)$$, то нормаль имеет вид $$(dy,-dx)$$ (для замкнутой границы предполагаем, что она обходися против часовой стрелки, а нормаль внешняя). Учтем, что

$$\displaystyle E^*=E_x-iE_y=-\frac{\partial\phi}{\partial x}+i\frac{\partial\phi}{\partial y}= -\frac{d\psi}{dz}. $$

Пишем

$$\displaystyle 4\pi Q=\int_S E_n\,dS=\int_S(E_x\,dy-E_y\,dx)= $$
$$\displaystyle =\int_S(E_x\,dy-E_y\,dx-i(E_x\,dx+E_y\,dy))= $$
$$\displaystyle =-i\int_S(E_x-iE_y)(dx+i\,dy)=i\int_S\frac{d\psi}{dz}\,dz. $$

(Добавленная мнимая часть равна нулю, поскольку потенциал проводника постоянный.) В общем-то довольно очевидная формула: тогда как поле определяется вещественной частью комплексного потенциала, заряд выражается через приращение мнимой части при обходе проводника.

Проще вычислить заряд в переменных $$w$$

$$\displaystyle 4\pi Q=i\ctg w|_{\pi/2+i\infty}^{\pi/2-i\infty}=-2. $$

Отметим, что особенность $$1/z$$ в двумерном случае представляет собой диполь. Потенциал имеет особенности такого типа в точках $$z=1/\pi n$$, $$n=1,2,\ldots$$, лежащих внутри трубы. Формально сумма зарядов любого конечного числа диполей равна нулю, но, как показано выше, заряд трубы не равен нулю. Видимо, аналогичное происходит в трехмерном случае: заряд шара формально расходится, но нужно сперва просуммировать ряд для поля, а потом уже вычислять заряд.


Ага, Миптер прав, инверсия позволяет написать ряд для потенциала и в трехмерном случае.
Последний раз редактировалось peregoudov 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
peregoudov
Сообщений: 1917
Зарегистрирован: 09 сен 2007, 21:00

Шарик на плоскости

Сообщение peregoudov » 19 янв 2013, 21:54

До кучи решение в трехмерном случае.

Пусть радиус сферы равен 1/2. Потенциал на бесконечности $$\phi=r\cos\theta+\ldots$$. Делаем инверсию $${\bf r}={\bf r}&#39;\!/r^{\prime2}$$, при этом $$\phi=r&#39;\phi&#39;$$. В штрихованных переменных область --- пластина $$0<z&#39;<1$$, при $$r&#39;\to0$$ особенность в потенциале $$\phi&#39;=\frac{\cos\theta}{r^{\prime2}}+\ldots$$ --- диполь. Методом изображений

$$\displaystyle \phi&#39;=\sum_{n=-\infty}^\infty\frac{z&#39;-2n}{|{\bf r}&#39;-2n{\bf e}_z|^3}. $$

В исходных переменных

$$\displaystyle \phi=\frac1{\sqrt{z^2+\rho^2}}\sum_{n=-\infty}^\infty\frac{\frac z{z^2+\rho^2}-2n}{\Bigl[\bigl(\frac z{z^2+\rho^2}-2n\bigr)^2+\frac{\rho^2}{(z^2+\rho^2)^2}\Bigr]^{3/2}}. $$

Плотность заряда будем вычислять не на шаре, а на плоскости. Очевидно, что отклонение плотности от равномерной при интегрировании как раз даст заряд шара с обратным знаком.

$$\displaystyle 4\pi\sigma=-\left.\frac{\partial\phi}{\partial z}\right|_{z=0}=-1-2\sum_{n=1}^\infty\frac{1-8\rho^2n^2}{(1+4\rho^2n^2)^{5/2}}. $$

Первый член тут как раз представляет постоянную плотность (которая имела бы место в отсутствие шара), поэтому заряд шара

$$\displaystyle 4\pi Q=2\sum_{n=1}^\infty\int_0^\infty2\pi\rho\,d\rho\,\frac{1-8\rho^2n^2}{(1+4\rho^2n^2)^{5/2}}= 2\sum_{n=1}^\infty\frac\pi{n^2}\int_0^\infty\frac{1-8\xi}{(1+4\xi)^{5/2}}\,d\xi=-\frac{\pi^3}6. $$

(При преобразовании сделана замена $$\rho^2n^2=\xi$$.)
Последний раз редактировалось peregoudov 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
balans
Сообщений: 2030
Зарегистрирован: 29 дек 2012, 21:00

Шарик на плоскости

Сообщение balans » 20 янв 2013, 08:29

Здравия Вам желаю.
Посокольку шарик и плоскость проводящи, то в равновеснов случае их потенциалы равны по всем участкам поверхностей. Расположим над шариком на расстоянии от его центра $$H$$ точечный электрический заряд $$Q$$. Тогда этот заряд создаст у поверхности напряженность
$$E=\frac {Q} {(R+H)^2}$$
при этом полагаем, что $$Q$$ и $$H$$ принимают очень большое значение.
Используем метод электрических изображении. Расположим зеркально, относительно поверхности, заряд $$-Q$$.
Заряд $$Q$$ индуцирует в шарике заряд

$$q&#39;=-\frac {R} {H}Q$$

Зеркальный заряд $$-Q$$ соответственно

$$q&#39;&#39;=\frac {R} {H+2R}Q$$.
Так как $$H$$ стремится в бесконечность, то индуцированные заряды распологаются в центрешарика и совмещаются

$$q=q&#39;+q&#39;&#39; =- \frac {R} {H}Q +\frac {R} {H+2R}Q$$.

Получаем
$$\lim \limits_{H,Q \to \infty} {q}=2R^2 E$$
Далее заряд $$q$$ отзеркалевается относительно плоскости и оказывается в центре мнимого шара. Естественно отражение этого заряда индуцирует еще один заряд (в зеркале отображено зеркала сзеркало и т. д.)
Полученная сумма имеет такой вид
$$q(1+\frac {1} {2}+\frac {1} {3}+\frac {1} {4}+\frac {1} {5}+...)=\infty$$

Может в чём и ошибся.
Последний раз редактировалось balans 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
lapay
Сообщений: 266
Зарегистрирован: 29 фев 2012, 21:00

Шарик на плоскости

Сообщение lapay » 20 янв 2013, 08:32

А кто может прокомментировать следующий результат?
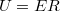
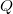
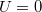
Будем рассматривать точку в центре шара. Пока нет шара, заряженная плоскость создаёт, в этой точке, разность потенциалов между этой точкой и плоскостью $$U=ER$$. Когда мы ставим шар, у нас заряд $$Q$$ переходит из плоскости на шар. Так как внутри шара нет поля, то потенциал в центра шара становится равным нулю $$U=0$$. 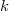Заряд, который перешёл на поверхность шара, создаёт потенциал $$U=\frac QR$$, для отрицательного заряда, который остался на плоскости, расстояние от зарядов до центра шарика $$R_1> R$$, поэтому суммарный потенциал этих зарядов будет $$U=k\frac QR=-ER$$, где $$k$$ это интегральный множитель, меньший единицы. Отсюда получается, что заряд на шарике будет отрицательный и довольно большой. Явно абсурдный результат, но ошибки, вроде, нет.
Проверим, для надёжности, как меняется суммарный заряд системы после внесения шарика. Шарик изменяет энергию системы на величину порядка плотности поля, умноженному на объём шарика $$\Delta A\approx E^2V_s$$. В то же время $$\Delta A=\frac{U^2\Delta C}{2}=\frac{U\Delta Q}{2}$$. Чем больше разность потенциалов конденсатора (расстояние между пластинами), тем меньшим будет изменение заряда системы, то есть, предположение, что заряд переходит из плоскости на шарик, правильное.

Кстати, если использовать метод изображений, то надо учитывать, что поверхность шарика то же проводящая, то есть, не только заряды шарика наводят "фантом" на плоскости, но и заряды плоскости наводят заряды на поверхности шара. Поэтому тут появляется нелинейность и такой путь заводит в непроходимые дебри.
Последний раз редактировалось lapay 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
Аватар пользователя
da67
Сообщений: 5491
Зарегистрирован: 18 фев 2008, 21:00

Шарик на плоскости

Сообщение da67 » 20 янв 2013, 09:11

lapay писал(а):Source of the post Так как внутри шара нет поля, то потенциал в центра шара становится равным нулю $$U=0$$.
Тут неверно.
Начните с одинокой заряженной сферы.
Последний раз редактировалось da67 28 ноя 2019, 15:04, всего редактировалось 1 раз.
Причина: test
Вернуться наверх
Ответить на сообщение

Вернуться в «Физика»

Кто сейчас на форуме

Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей