КМ. Спин.
Добавлено: 18 май 2011, 20:35
Здравствуйте!
Вывожу оператор конечного поворота вокруг оси z. Делаю так:
повернём систему на малый угол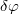 . Тогда
. Тогда

Далее выделяю последнее слагаемое. Переобозначаю за какое-нибудь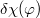
Далее,

Получаю

Дальше, взбрело в голову посмотреть ЛЛ. Посмотрел. Как всегда. Почему у него написано так:

Причём, они вроде как делали как я. Что у него тогда такое (имется ввиду не обозначения букв, а именно штрих, т.к. он мне непонятно откуда взялся) и как он нашёл константу (я так полагаю, что при фи = 0 волн. ф-я должна совпадать сама с собой)? Понимаю, что вопросы тупые и, наверняка, очевидные, но тем не менее.
(имется ввиду не обозначения букв, а именно штрих, т.к. он мне непонятно откуда взялся) и как он нашёл константу (я так полагаю, что при фи = 0 волн. ф-я должна совпадать сама с собой)? Понимаю, что вопросы тупые и, наверняка, очевидные, но тем не менее.
Вывожу оператор конечного поворота вокруг оси z. Делаю так:
повернём систему на малый угол
Далее выделяю последнее слагаемое. Переобозначаю за какое-нибудь
Далее,
Получаю
Дальше, взбрело в голову посмотреть ЛЛ. Посмотрел. Как всегда. Почему у него написано так:
Причём, они вроде как делали как я. Что у него тогда такое