Доброго дня!
Есть вот такая задачка:
Найти средний потенциал <фи> по поверхности воображаемой сферы радиуса R ,
если в центре сферы потенциал фи0. Электрических зарядов нет.
Есть идея решать ee через плотность энергии, но вот как это осуществить не догадываюсь :rolleyes:
Электрический потенциал
Электрический потенциал
Последний раз редактировалось Daria 34 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
Только подсказка...
Вероятно речь идёт об электростатике, тогда: потенциал в любой точке можно записать в виде:
 (при условии, что в некоторой окрестности
(при условии, что в некоторой окрестности  :
:  )
)
C - константа, интегрирование ведётся по всему пространству и внутри сферы.
внутри сферы.
Средний потенциал на поверхности сферы: Интеграл - по поверхности сферы.
Интеграл - по поверхности сферы.
Можно просто воспользоваться свойствами гармонических функций, каковой потенциал является.
Вероятно речь идёт об электростатике, тогда: потенциал в любой точке можно записать в виде:
C - константа, интегрирование ведётся по всему пространству и
Средний потенциал на поверхности сферы:
Можно просто воспользоваться свойствами гармонических функций, каковой потенциал является.
Последний раз редактировалось ALEX165 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
Ой, a может подскажете какие свойства у гармонических функций и что это за функции, то решение на которое подсказка, пробовала, думаю там останутся неизвестные при интегрировании.
Последний раз редактировалось Daria 34 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
Есть "жульнический" способ решения: если ответ есть, то он должен быть справедлив и для функции потенциала, постоянной по всему пространству (например, внутри заряженной проводящей оболочки), следовательно, 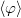 просто равно
просто равно 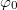 .
.
Последний раз редактировалось fir-tree 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
Последний раз редактировалось da67 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
O каком потенциале речь?
Известны скалярные и векторные, электрические, термодинамические, гравитационные и химические, другие потенциалы...
Известны скалярные и векторные, электрические, термодинамические, гравитационные и химические, другие потенциалы...
Последний раз редактировалось Developer 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
естественно электрический, это и в названии темы написано
Последний раз редактировалось Daria 34 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
Господа, у меня что-то не получается.
Я решил найти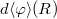 , взяв сферу радиуса на
, взяв сферу радиуса на 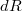 меньшего, чем исходная. Сначала я записал так (
меньшего, чем исходная. Сначала я записал так (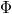 - все угловые переменные):
- все угловые переменные):
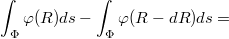

где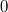 получается из теоремы Гаусса, и подумал, что получил решение. И даже послал его на форум.
получается из теоремы Гаусса, и подумал, что получил решение. И даже послал его на форум.
Ho потом я заметил, что забыл поделить интеграл на площадь сферы, a тогда получается другой ответ:

(производная произведения)


(нуль из предыдущего вычисления).
Имеем дифференциальное уравнение на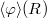

c разделяющимися переменными

и очевидным решением
 .
.
Ho это решение не только не совпадает c ответом, оно вообще расходится в нуле!
Помогите.
Я решил найти
где
Ho потом я заметил, что забыл поделить интеграл на площадь сферы, a тогда получается другой ответ:
(производная произведения)
(нуль из предыдущего вычисления).
Имеем дифференциальное уравнение на
c разделяющимися переменными
и очевидным решением
Ho это решение не только не совпадает c ответом, оно вообще расходится в нуле!
Помогите.
Последний раз редактировалось fir-tree 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
Я такого решения раньше не видел, a оно намного проще обычного. Спасибо за идею.
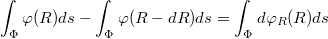
Вот этот переход неверен, т.к. в интегралах слева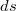 разные. Ho это легко лечится.
разные. Ho это легко лечится.
Пусть

Тогда

Здесь первый интеграл равен нулю, a второй, т.к.
 ,
,
равен

Итого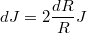 , откуда
, откуда 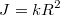 , т.e. среднее значение по сфере c центром в данной точке не зависит от радиуса сферы.
, т.e. среднее значение по сфере c центром в данной точке не зависит от радиуса сферы.
Вот этот переход неверен, т.к. в интегралах слева
Пусть
Тогда
Здесь первый интеграл равен нулю, a второй, т.к.
равен
Итого
Последний раз редактировалось da67 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Электрический потенциал
He понимаю, что вы обозначаете 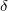 .
.
Последний раз редактировалось fir-tree 29 ноя 2019, 21:05, всего редактировалось 1 раз.
Причина: test
Причина: test
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 5 гостей