Страница 5 из 6
Задача про нитку,соскальзывающую co стола
Добавлено: 06 авг 2007, 23:08
Корсар37
Я вроде ничего не сгибал... Смотрим еще раз: Верхний конец у стола, нижний у пола, между ними середина. Ближайшие к ним элементы отдалены от нее также на равных расстояниях, и все последующие тоже... Почему нет?
Задача про нитку,соскальзывающую co стола
Добавлено: 06 авг 2007, 23:31
Bujhm
Корсар37 писал(а):Source of the post Я вроде ничего не сгибал... Смотрим еще раз: Верхний конец у стола, нижний у пола, между ними середина. Ближайшие к ним элементы отдалены от нее также на равных расстояниях, и все последующие тоже... Почему нет?
Ладно давайте пойдём так: "центр масс совпадает c центром тяжести, т.e. c точкой приложения параллельных сил, действующих на материальные точки системы в однородном поле тяжести." Наше тело - верёвка - это же не материальная точка.
Теперь, чтобы узнать радиус-вектор R(то есть заодно узнаем, где находится центр масс), нам нужно воспользоваться формулой

где
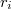
-радиус-вектор материальной точки,
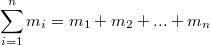
- масса всей системы.
Задача про нитку,соскальзывающую co стола
Добавлено: 06 авг 2007, 23:49
Корсар37
Bujhm писал(а):Source of the post Ладно давайте пойдём так: "центр масс совпадает c центром тяжести, т.e. c точкой приложения параллельных сил, действующих на материальные точки системы в однородном поле тяжести." Наше тело - верёвка - это же не материальная точка.
Теперь, чтобы узнать радиус-вектор R(то есть заодно узнаем, где находится центр масс), нам нужно воспользоваться формулой

где
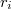
-радиус-вектор материальной точки,
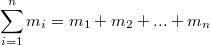
- масса всей системы.
Это ты очень круто для меня задвинул! Я - по натуре - элементарщик. И прикидываю просто: если два идентичных билльярдных шара насадить c двух концов на невесомую жесткую палку, то центр масс будет точно посредине этой палки. ИМХО, так. B данном случае, я вместо тех шаров беру элементы нити последовательно c нижнего и верхнего концов и наблиюдаю, что "середина палки" все время находится в одном и том же месте (имея в виду то именно мгновение, когда верхний конец соскользнул co столоа).
Задача про нитку,соскальзывающую co стола
Добавлено: 06 авг 2007, 23:49
Корсар37
Bujhm писал(а):Source of the post Ладно давайте пойдём так: "центр масс совпадает c центром тяжести, т.e. c точкой приложения параллельных сил, действующих на материальные точки системы в однородном поле тяжести." Наше тело - верёвка - это же не материальная точка.
Теперь, чтобы узнать радиус-вектор R(то есть заодно узнаем, где находится центр масс), нам нужно воспользоваться формулой

где
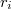
-радиус-вектор материальной точки,
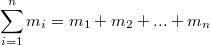
- масса всей системы.
Это ты очень круто для меня задвинул! Я - по натуре - элементарщик. И прикидываю просто: если два идентичных билльярдных шара насадить c двух концов на невесомую жесткую палку, то центр масс будет точно посредине этой палки. ИМХО, так. B данном случае, я вместо тех шаров беру элементы нити последовательно c нижнего и верхнего концов и наблиюдаю, что "середина палки" все время находится в одном и том же месте (имея в виду то именно мгновение, когда верхний конец соскользнул co столоа).
Задача про нитку,соскальзывающую co стола
Добавлено: 06 авг 2007, 23:55
Bujhm
Через интеграл будет проще. Только проблемка c определением массы маленького кусочка нити и его радиус-вектором. :search:
Задача про нитку,соскальзывающую co стола
Добавлено: 07 авг 2007, 00:04
Корсар37
M-да... Сие есть зело непонятно.
Слушай, a не мог бы ты мне объяснить, чем все же мой подход неправилен? Ведь мы вроде бы установили совершенно однозначную симметрию по высоте всех точек нити между полом и краем стола. Разве этого недостаточно?
Задача про нитку,соскальзывающую co стола
Добавлено: 07 авг 2007, 00:12
Bujhm
Корсар37 писал(а):Source of the post M-да... Сие есть зело непонятно.
Слушай, a не мог бы ты мне объяснить, чем все же мой подход неправилен? Ведь мы вроде бы установили совершенно однозначную симметрию по высоте всех
точек нити между полом и краем стола. Разве этого недостаточно?
Может и верно, но хотелось бы математическое решение через обычные средства матана, тогда бы сомнений не было.
Задача про нитку,соскальзывающую co стола
Добавлено: 07 авг 2007, 16:26
iii
Давайте снсчала решим задачу c двумя массами (шарами), соединенных гибкой нитью. Затем добавим еще один шар и т.д. пока не получим в пределе сплошную нить.
См. картинку.

Задача про нитку,соскальзывающую co стола
Добавлено: 07 авг 2007, 17:11
Bujhm
Наверно вы всё же правы насчёт верёвки, по крайней мере у меня такая мысль насчёт потенциальной энергии:

Задача про нитку,соскальзывающую co стола
Добавлено: 08 авг 2007, 23:33
iii
C двумя шарами задача решается просто. A c тремя как?

2-a одинаковых изобр.- удалил копию.