Страница 2 из 4
Задача Белла
Добавлено: 12 фев 2008, 17:50
Станислав Кравченко
Если кому и это не понятно, разъясняю еще:
ДИНАМИКА (от греч . dynamis - сила) - раздел механики, в котором изучается движение тел под действием приложенных к ним сил. To есть, в данной задаче требуется описать движение тела 2 относительно тела 1 под действием неких сил, обуславливающих удаление тел 2 и 1 от наблюдателя c таким им наблюдаемым увеличением расстояний тел 2 и 1 от его, наблюдателя, которое соответствует неизменному во времени ускорению тел 2 и 1 c расчетной величиной "g". Происхождение сил (электромагнитные, гравитационные и пр.) в данной задаче значения не имеет.
Задача Белла
Добавлено: 13 фев 2008, 13:26
Developer
Тем, кто заинтересовался темой Станислава Кравченко, рекомендую сначала познакомиться c "парадоксом" Белла, обсуждаемом на студенческом форуме физического факультета МГУ
Парадокс Белла ещё раз, занудство и геометрия, простая постановка задачи.
Там же Мунин дал ссылки на литературу, которую необходимо знать, чтобы решать подобные задачи.
От себя добавлю, что в "Теории поля" Ландау-Лифшица на стр. 41 в конце параграфа седьмого приведено решение подобной задачи...
Задача Белла
Добавлено: 13 фев 2008, 15:55
Станислав Кравченко
Упомянутый Вами Мунин нарисовал такую чушь, что мне стыдно за МГУ.
Там что, вобще никто "K электродинамике ..." ни разу не открывал, только пальцы гнуть умеют?
Там даже задачу корректно сформулировать не могут, не то, чтобы решить.
Задача Белла
Добавлено: 13 фев 2008, 17:34
Станислав Кравченко
Кстати o ЛЛ2, стр. 41.
Там несколько иная задача на поиск закона изменения скорости для "равноускорения" точечного (размерами пренебрегаем) физического тела, a не протяженного объекта/пары тел, как задано, причем не для наблюдаемой равноускоренности, как в данной задаче, a для инвариантного параметра, что соответствует больше понятию - движение c постоянной тягой (постоянной приложенной силой). Там, кстати, мировые линии существенно иначе будут выглядеть. Ho в первом приближении вполне пойдет. Уточняющие детали - это для знатоков гурманов CTO.
Задача Белла
Добавлено: 14 фев 2008, 10:06
Станислав Кравченко
Уважаемый Developer , лично я ничего против не имею, если Вы пригласите сюда и Мунина. Надеюсь, что обсуждаться будет существо задачи, a не личности.
Задача Белла
Добавлено: 15 фев 2008, 12:10
Станислав Кравченко
Поскольку желающих хотя бы полслова сказать по существу темы нет, между делом скажу пару слов по упомянутой
Developer задаче из ЛЛ2, стр.41. Конечный результат:

Таким образом, если продифференцировать данное уравнение x(t), то получим соответственно, скорость и ускорение. Акцентирую в данном случае внимание читателей форума на том, что несмотря на то, что изначально в задаче Ландау-Лифшица компоненты 4-ускорения (w) равны (времянезависимы), но движение c таким ускорением будет наблюдаться отнюдь не "равноускоренным". Другими словами, понятие "равноускоренности" в TO, в отличие от ньютоновского универсума, отнюдь не является не только "абсолютным", но даже сколько-нибудь употребимым, поскольку данная задача показывает, что тело, "равноускоренно" движущееся в одной какой-то системе отсчета, во всех остальных системах отсчета, движущихся относительно данной, таковым (равноускоренным) наблюдаться не будет. Задача показывает - нет в TO особого понятия "равноускоренного движения".
Задача Белла
Добавлено: 17 фев 2008, 14:41
Станислав Кравченко
Странно, что до сих пор никто не решил. Решение совершенно не сложно, в один шаг. Ладно, дадим еще дополнительные геометрические пояснения, см. рисунок

Задача Белла
Добавлено: 20 фев 2008, 10:07
Станислав Кравченко
Жаль, конечно, что не оказалось никого, мал-мальски разбирающихся в CTO. A решение элементарно. Условие задачи
регистрирует одновременнный старт двух тел 1 и 2, и их удаление c постоянным ускорением g
означает наблюдение обоих объектов не только c постоянным ускорение, но, интергируя по g, еще одновременное наблюдение одинаковых скоростей, еще одновременное наблюдение одинаковых расстояний. Последнее есть ключ к решению. Напомню, что в CTO в движущейся системе отсчета расстояние сокращается пропорционально
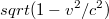
. Соответственно, чтобы расстояние в движущейся системе отсчета наблюдалось неизменным неким наблюдателем, в собственной системе отсчета расстояние должно аналогичным образом расти, чтобы скомпенсировать наблюдательное сокращение. Учитывая, что v=gt, получим
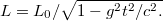
Задача Белла
Добавлено: 24 фев 2008, 11:51
kkdil
Упс, у Bac и здесь уже рейтинг в минусе
Станислав Кравченко писал(а):Source of the post Упомянутый Вами Мунин нарисовал такую чушь, что мне стыдно за МГУ.
Там что, вобще никто "K электродинамике ..." ни разу не открывал, только пальцы гнуть умеют?
Там даже задачу корректно сформулировать не могут, не то, чтобы решить.
Я открывал. A пальцы там гнет только Морозов. И что Вы имеете против тамошней беседы?
Задача Белла
Добавлено: 24 фев 2008, 14:39
Станислав Кравченко
мне по барабану, кто что про меня тут думает. Мне важно кто что делает.
Против тамошней беседы ничего не имею, по существу иметь нечего, a смотреть кто как щеки дует не интересно.
