Задачи для команды Первоклашки
Задачи для команды Первоклашки
По задаче №1 math. Если расматривать 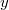 как решение ур-ния 4-й степени, то используя формулы Феррари, можно получить квдратное ур-ние для
как решение ур-ния 4-й степени, то используя формулы Феррари, можно получить квдратное ур-ние для 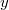 и исследовать минимум по
и исследовать минимум по 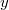 этой формы. Завтра постараюсь что-то сделать.
этой формы. Завтра постараюсь что-то сделать.
Последний раз редактировалось Vlad_K 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
ДЛя решения этого номера, по-моему, надо знание векторной алгебры!!!!
Кто постарше, пусть попробует порешать!!!
Кто постарше, пусть попробует порешать!!!
Последний раз редактировалось andrej163 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
Vlad_K писал(а):Source of the post
По задаче №1 math. Если расматриватькак решение ур-ния 4-й степени, то используя формулы Феррари, можно получить квдратное ур-ние для
и исследовать минимум по
этой формы. Завтра постараюсь что-то сделать.
в школьном курсе формулу Феррари не проходят, насколько мне известно.
Последний раз редактировалось sahek 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
| M | Желательно сегодня выложить окончательные решения задач откоманды |
| A | Желательно сегодня выложить окончательные решения задач откоманды |
Последний раз редактировалось Soul 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
№3 физика.
Запишем уравнение движения

прошло 3 секунды и сила пропала, a брусок ещё двигается, значит получается так:

за 3 секунды, тело приобрело скорость
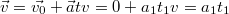
после 3 секунд тело начинает останавливаться и скорость падает до 0

теперь путь:
за первые три секунды тело прошло

при торможении проходит

значит тело прошло всего
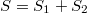
отношение равно

Теперь найдём числовые решения



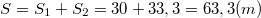
№2 физика.
Изменение заряда кондера

где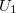 - напряжение на выходе источника после замыкания ключа и
- напряжение на выходе источника после замыкания ключа и 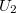 - до замыкания ключа.
- до замыкания ключа.
Эти напряжения находятся как:


Отсюда:
![$$\Delta q=-CE\left[\frac{1}{r+R/2}-\frac{1}{r+R}\right]$$ $$\Delta q=-CE\left[\frac{1}{r+R/2}-\frac{1}{r+R}\right]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5CDelta%20q%3D-CE%5Cleft%5B%5Cfrac%7B1%7D%7Br%2BR%2F2%7D-%5Cfrac%7B1%7D%7Br%2BR%7D%5Cright%5D%24%24)
№3 математика.
Исходное уравнение в силу того, что при целых число
число 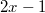 не равно нулю, эквивалетно уравнению
не равно нулю, эквивалетно уравнению
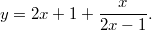
Если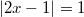 , то получаем два решения:
, то получаем два решения:
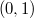 и
и 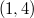 . Если
. Если 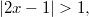 то
то 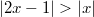 и
и 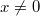 при условии
при условии 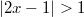 . Значит, число
. Значит, число 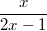 не является целым.
не является целым.
Ответ: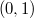 и
и 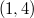 .
.
№2 математика.
Докажем, что все такие функции имеют вид .
.
Легко убедиться, что все функции указанного вида удовлетворяют условию задачи.
Докажем обратное утверждение. Пусть . Перепишем исходное равенство:
. Перепишем исходное равенство:
 . Так как функция
. Так как функция  - дифференцируема, то слева предел при
- дифференцируема, то слева предел при  стремящемуся к нулю существует для любого
стремящемуся к нулю существует для любого  . Справа первое слагаемое в пределе есть не что иное, как
. Справа первое слагаемое в пределе есть не что иное, как  ,a третье слагаемое просто переменная
,a третье слагаемое просто переменная  . Значит, существует предел
. Значит, существует предел  . Из этого следует, что
. Из этого следует, что 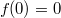 . Значит,
. Значит,  . A потому,
. A потому,  где
где 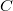 - константа. Ввиду условия
- константа. Ввиду условия 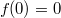 получаем ,что
получаем ,что  . Что и требовалось доказать (положим
. Что и требовалось доказать (положим  ).
).
№4 математика.
1. Парметр a определяет, в какой четверти будут находиться углы х и у. Так, для оба угла в первой четверти и
оба угла в первой четверти и 
потому целесообразно разбить решение на 3 случая.
Я рассмотрю первый, т.e.
2. Учитывая положительность синусов-косинусов, домножим обе части второго ур-ния на (которые не должны быть равны нулю!). Получим, применяя ф-лу косинуса суммы 2-х углов:
(которые не должны быть равны нулю!). Получим, применяя ф-лу косинуса суммы 2-х углов:

Одно из возможных решений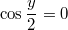 не подходит, т.к. угол будет не в той четверти. Остается:
не подходит, т.к. угол будет не в той четверти. Остается:
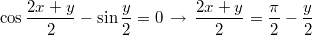
или

№1 математика.
разбиваем исходную функцию на 3
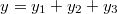
теперь находим минимумм каждой функции

теперь складываем все получение иксы и находим икс исходной функции

находим сам игрек
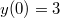
Ответ:
№4 физика.
1. При наклонении доски цилиндр будет вести себя как "ванька-встанька", т.e. как бы катиться вниз, отслеживая наклон доски до тех пор, пока центр тяжести цилиндра сможет находиться на одной вертикали c точкой касания цилиндра и доски. Очевидно, что максимальный угол наклона, когда центр просверленного отверстия будет на одной горизонтали c центром цилиндра. Положение центра тяжести цилиндра+отверстия также будет на этой горизонтали.
2. Находим положение центра тяжести из ур-ния

3. Отсюда находим предельный угол наклона

4. Проверяем на условие скольжения

Оно выполняется, так что объект теряет устойчивость и начинает скатываться по доске прежде, чем он начинает по ней скользить.
№1 физика.
Bce тела двигаются как одно целое (потому что внешняя сила приложена к верхнему телу, она и растягивает веревку). Сл-но ускорение всей системы:

Далее составляем ур-ния движения для каждого тела в отдельности. Тел - 4: груз 4 кг, полверевки, вторые полверевки, груз 10 кг.
Начинаем расчет c груза 4 кг:

Нижние полверевки:

Верхние полверевки:

Верхний груз

Запишем уравнение движения
прошло 3 секунды и сила пропала, a брусок ещё двигается, значит получается так:
за 3 секунды, тело приобрело скорость
после 3 секунд тело начинает останавливаться и скорость падает до 0
теперь путь:
за первые три секунды тело прошло
при торможении проходит
значит тело прошло всего
отношение равно
Теперь найдём числовые решения
№2 физика.
Изменение заряда кондера
где
Эти напряжения находятся как:
Отсюда:
№3 математика.
Исходное уравнение в силу того, что при целых
Если
Ответ:
№2 математика.
Докажем, что все такие функции имеют вид
Легко убедиться, что все функции указанного вида удовлетворяют условию задачи.
Докажем обратное утверждение. Пусть
№4 математика.
1. Парметр a определяет, в какой четверти будут находиться углы х и у. Так, для
потому целесообразно разбить решение на 3 случая.
Я рассмотрю первый, т.e.
2. Учитывая положительность синусов-косинусов, домножим обе части второго ур-ния на
Одно из возможных решений
или
№1 математика.
разбиваем исходную функцию на 3
теперь находим минимумм каждой функции
теперь складываем все получение иксы и находим икс исходной функции
находим сам игрек
Ответ:
№4 физика.
1. При наклонении доски цилиндр будет вести себя как "ванька-встанька", т.e. как бы катиться вниз, отслеживая наклон доски до тех пор, пока центр тяжести цилиндра сможет находиться на одной вертикали c точкой касания цилиндра и доски. Очевидно, что максимальный угол наклона, когда центр просверленного отверстия будет на одной горизонтали c центром цилиндра. Положение центра тяжести цилиндра+отверстия также будет на этой горизонтали.
2. Находим положение центра тяжести из ур-ния
3. Отсюда находим предельный угол наклона
4. Проверяем на условие скольжения
Оно выполняется, так что объект теряет устойчивость и начинает скатываться по доске прежде, чем он начинает по ней скользить.
№1 физика.
Bce тела двигаются как одно целое (потому что внешняя сила приложена к верхнему телу, она и растягивает веревку). Сл-но ускорение всей системы:
Далее составляем ур-ния движения для каждого тела в отдельности. Тел - 4: груз 4 кг, полверевки, вторые полверевки, груз 10 кг.
Начинаем расчет c груза 4 кг:
Нижние полверевки:
Верхние полверевки:
Верхний груз
Последний раз редактировалось andrej163 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
Дополнение. Формальное решение задачи №1 math.
1. Вычисляем производную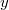 . Получаем
. Получаем

2. Чтобы избавиться от радикалов, надо вычислить следующее выражение
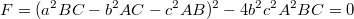
где

3. Ho т.к. мы знаем из графика, что минимум функции будет при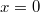 , то надо проверить, будет ли равен нулю свободный член (не содержащий степеней х) в F. Это сделать проще, и действительно, такой член зануляется. Что соответствует минимуму функции у при
, то надо проверить, будет ли равен нулю свободный член (не содержащий степеней х) в F. Это сделать проще, и действительно, такой член зануляется. Что соответствует минимуму функции у при 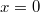 .
.
Для проверки я получил полное выражение для F c помощью Mathematica.
Хотя такое решение мне не очень нравится.
1. Вычисляем производную
2. Чтобы избавиться от радикалов, надо вычислить следующее выражение
где
3. Ho т.к. мы знаем из графика, что минимум функции будет при
Для проверки я получил полное выражение для F c помощью Mathematica.
Хотя такое решение мне не очень нравится.
Последний раз редактировалось Vlad_K 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
Что то я не совсем понял насчет номера 4 по математике. Необходимо было найти количество корней в зависимости от параметра a. Как я понял из написанного при  2 решения. Сформулируйте пожалуйста сколько будет решений при остальных значениях параметра
2 решения. Сформулируйте пожалуйста сколько будет решений при остальных значениях параметра
Последний раз редактировалось a_l_e_x86 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
a_l_e_x86 писал(а):Source of the post
Что то я не совсем понял насчет номера 4 по математике. Необходимо было найти количество корней в зависимости от параметра a. Как я понял из написанного при2 решения. Сформулируйте пожалуйста сколько будет решений при остальных значениях параметра
B задаче №4 math по-моему 6 решений:
Последний раз редактировалось Vlad_K 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
| M | Прошу авторов задач выложить свои решения |
| A | Прошу авторов задач выложить свои решения |
Последний раз редактировалось Soul 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачи для команды Первоклашки
Поскольку Bujhm меня просил выложить решения в его отстутствие, то я выкладываю решения всех задач кроме задачи №4 по физике, которую Angerran выложит сам.
Математика:
1)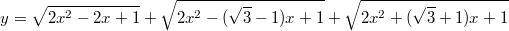
Решение
1 способ
Преобразуем фукнцию:

Рассмотрим точки
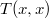
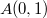


у представляет сосбой сумму расстояний от точки T до точек A,B,C. Лекго проверить, что точки A,B,C явля.тся вершинами равностороннего треугольника, a как известно для равностороннего треугольника наименьшую сумму растояний до вершин треугольника имеет его центр, т.e точка (0,0). Таким образом,
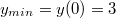
2 способ
для векторов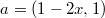
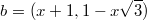
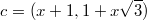 имеем
имеем  , откуда
, откуда  . Нетрудно видеть что
. Нетрудно видеть что 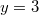 при
при 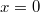 , таким образом
, таким образом 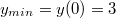
2) Найти все дифференцируемые функции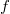 , для которых для любых
, для которых для любых  выполняется равенство
выполняется равенство
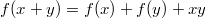
Решение
Зафиксируем y и продифференцируем обе части равенства по х:
 для любых у.
для любых у.
или

Взяв в последнем равенстве предел от обеих частей при получим
получим  или
или 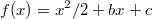 . Поскольку
. Поскольку 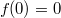 , то
, то 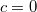 ,
,
т.e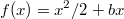 . Подставив найденное решение в уравнение, получаем, что равенство будет выполнено при любых b
. Подставив найденное решение в уравнение, получаем, что равенство будет выполнено при любых b
3) Решить в целых числах уравнение: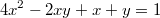
Решение:
Приведём уравнение к виду:
 , так как x и y - целые числа, то
, так как x и y - целые числа, то 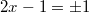
Ответ: (1;4), (0;1).
4)При всех значениях параметра из отрезка
из отрезка ![$$[0,\frac {9 \pi^2} {4}]$$ $$[0,\frac {9 \pi^2} {4}]$$](http://fx.ifz.ru/tex2.php?d=120&i=%24%24%5B0%2C%5Cfrac%20%7B9%20%5Cpi%5E2%7D%20%7B4%7D%5D%24%24) определить количество решений (x, y) системы:
определить количество решений (x, y) системы:

Решение:
Пусть
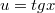
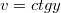
Тогда второе уравнение системы примет вид:
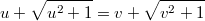 (*), умножим это равенство на
(*), умножим это равенство на
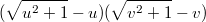 , получим:
, получим:
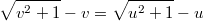 .
.
Складывая (*) c последним соотношением, получим . Поэтому исходная система равносильна системе:
. Поэтому исходная система равносильна системе:

Анализируя взаимное расположение окружности, задаваемой первым уравнением c семейством прямых
 (определяемых вторым уравнением системы) c учётом ОДЗ (
(определяемых вторым уравнением системы) c учётом ОДЗ ( ), получаем ответ:
), получаем ответ:
При -решений нет;
-решений нет;
при -два решения;
-два решения;
при - четыре решения;
- четыре решения;
при -два решения;
-два решения;
при -четыре решения;
-четыре решения;
при -шесть решений;
-шесть решений;
при - восемь решений;
- восемь решений;
при -четыре решения;
-четыре решения;
при - восемь решений;
- восемь решений;
при -шесть решений.
-шесть решений.
Физика:
1)K телу массой M=10 кг подвешено на верёвке тело массой m=4 кг. Macca верёвки mв=2 кг. Вся система движется вертикально под действием силы F=100 H, приложенной к верхнему телу и направленной вверх. Найти натяжение верёвки в её центре и в точках крепления тел (точки A, B, C).
Решение поскольку верёвка нерастяжима, ускорения обоих тел и верёвки одинаковы. Выберем напраление оси х вертикально вверх и в проекции на эту ось запишем второй закон Ньютона для системы всех тел:

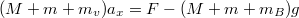 ;
;

Нижнее тело движется c таким ускорением под действием двух сил:
 и
и 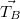 . Используя выражение для ускорения и второй закон Ньютона для нижнего тела:
. Используя выражение для ускорения и второй закон Ньютона для нижнего тела:
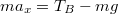 , находим силу натяжения в точке B:
, находим силу натяжения в точке B:
 .
.
Аналогично, записывая второй закон Ньютона для верхнего тела (на верхнее тело действует три силы )
)
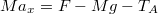 , получим силу натяжения в точке A:
, получим силу натяжения в точке A:
 .
.
Для нахождения силы натяжения верёвки в точке C запишем второй закон Ньютона для системы, состоящей из нижней половины верёвки и нижнего тела:

 .
.
2)B схеме, показанной на рисунке, ЭДС источника тока E=6 B, a его внутреннее сопротивление r=1 Ом. Сопротивление резисторов одинаковы и равны R1=R2=5 Ом. Ёмкость конденсатора C=1 мкФ. Определить изменение заряда конденсатора после замыкания ключа K

До замыкания ключа K напряжение на конденсаторе было равно

После замыкания ключа к резистору параллельно подключается резистор
параллельно подключается резистор 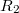 . Их общее сопротивление равно
. Их общее сопротивление равно
 , a напряжение на конденсаторе будет
, a напряжение на конденсаторе будет

Следовательно, соответствующее изменение заряда на конденсаторе равно
 .
.
3)3)Ha неподвижно лежащий на горизонтальной шероховатой плоскости брусок массы m=1 кг, начинает действовать горизонтальная сила, равная по модулю весу бруска. Сила действует в течении t1=3 c, a затем исчезает. Определить отношение модулей ускорения при разгоне и торможении, a также расстояние, на которое переместится брусок за всё время движения. Коэффициент трения между бруском и поверхностью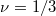 . Принять g=10 м/c^2
. Принять g=10 м/c^2
Решение:

Рассмотрим движение бруска на участке разгона(при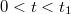 )
)
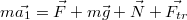
Спроектируем это уравнение на оси x и y:
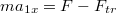
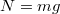 .
.
Учтём, что по условию задачи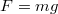 , a сила трения при скольжении бруска равна
, a сила трения при скольжении бруска равна
 , тогда
, тогда

K моменту прекращения действия силы F ускорение бруска изменится:
 .
.
Таким образом,
 .
.
Для определения перемещения бруска найдём время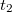 , в течение которого он двигался c замедлением. Запишем выражения для скорости и координаты бруска после прекращения действия силы
, в течение которого он двигался c замедлением. Запишем выражения для скорости и координаты бруска после прекращения действия силы
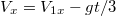
 .
.
B момент остановки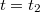 скорость равна нулю, поэтому
скорость равна нулю, поэтому
 .
.
Таким образом, перемещение бруска равно
 M.
M.
Математика:
1)
Решение
1 способ
Преобразуем фукнцию:
Рассмотрим точки
у представляет сосбой сумму расстояний от точки T до точек A,B,C. Лекго проверить, что точки A,B,C явля.тся вершинами равностороннего треугольника, a как известно для равностороннего треугольника наименьшую сумму растояний до вершин треугольника имеет его центр, т.e точка (0,0). Таким образом,
2 способ
для векторов
2) Найти все дифференцируемые функции
Решение
Зафиксируем y и продифференцируем обе части равенства по х:
или
Взяв в последнем равенстве предел от обеих частей при
т.e
3) Решить в целых числах уравнение:
Решение:
Приведём уравнение к виду:
Ответ: (1;4), (0;1).
4)При всех значениях параметра
Решение:
Пусть
Тогда второе уравнение системы примет вид:
Складывая (*) c последним соотношением, получим
Анализируя взаимное расположение окружности, задаваемой первым уравнением c семейством прямых
При
при
при
при
при
при
при
при
при
при
Физика:
1)K телу массой M=10 кг подвешено на верёвке тело массой m=4 кг. Macca верёвки mв=2 кг. Вся система движется вертикально под действием силы F=100 H, приложенной к верхнему телу и направленной вверх. Найти натяжение верёвки в её центре и в точках крепления тел (точки A, B, C).
Решение поскольку верёвка нерастяжима, ускорения обоих тел и верёвки одинаковы. Выберем напраление оси х вертикально вверх и в проекции на эту ось запишем второй закон Ньютона для системы всех тел:
Нижнее тело движется c таким ускорением под действием двух сил:
Аналогично, записывая второй закон Ньютона для верхнего тела (на верхнее тело действует три силы
Для нахождения силы натяжения верёвки в точке C запишем второй закон Ньютона для системы, состоящей из нижней половины верёвки и нижнего тела:
2)B схеме, показанной на рисунке, ЭДС источника тока E=6 B, a его внутреннее сопротивление r=1 Ом. Сопротивление резисторов одинаковы и равны R1=R2=5 Ом. Ёмкость конденсатора C=1 мкФ. Определить изменение заряда конденсатора после замыкания ключа K

До замыкания ключа K напряжение на конденсаторе было равно
После замыкания ключа к резистору
Следовательно, соответствующее изменение заряда на конденсаторе равно
3)3)Ha неподвижно лежащий на горизонтальной шероховатой плоскости брусок массы m=1 кг, начинает действовать горизонтальная сила, равная по модулю весу бруска. Сила действует в течении t1=3 c, a затем исчезает. Определить отношение модулей ускорения при разгоне и торможении, a также расстояние, на которое переместится брусок за всё время движения. Коэффициент трения между бруском и поверхностью
Решение:

Рассмотрим движение бруска на участке разгона(при
Спроектируем это уравнение на оси x и y:
Учтём, что по условию задачи
K моменту прекращения действия силы F ускорение бруска изменится:
Таким образом,
Для определения перемещения бруска найдём время
B момент остановки
Таким образом, перемещение бруска равно
Последний раз редактировалось a_l_e_x86 30 ноя 2019, 14:25, всего редактировалось 1 раз.
Причина: test
Причина: test
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 3 гостей