опять класс. мех.

4 8 15... · Сообщение **4 8 15...** » 13 окт 2011, 15:44

Уважаемые форумчане, нужна помощь!
Вот. Точка в центрально-симметричном поле, ее энергия в этом поле V( r ). Пишем Лагранжиан
$L=\dfrac{m}{2}(\dot{r}^2+r^2 \dot{\theta}^2)-V(r).~~P_\theta=Const=mr^2 \dot{\theta}~~=> L=\dfrac{m}{2}\dot{r}^2+\dfrac{P_\theta ^2}{2mr^2}-V(r)$ . Теперь допустим, что у какой-то другой точки, которая находится так же в неком поле, такой же лагранжиан, ее потенциальная энергия равна $-\dfrac{P_\theta ^2}{2mr^2}+V(r)$ . r-обычная координата в инерциальной системе. Т.к. оба лагранжиана равны, то и зависимость r(t) должна быть у обоих одинакова. Пусть $V(r)=-\dfrac{\alpha}{r}$ . 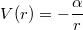Посмотрев на график потенциальной эн. второй точки, я понимаю, что зависимость r(t) все-таки разная у обоих точек. А где что не так?

ALEX165 · Сообщение **ALEX165** » 13 окт 2011, 15:54

4 8 15... писал(а):Source of the post
Т.к. оба лагранжиана равны, то и зависимость r(t) должна быть у обоих одинакова.

Не вникая во всё остальное - это, очевидно, неверно.
Даже у одной и той же системы со своим единственным лагранжианом может быть бесконечно много различных зависимостей r(t).

4 8 15... · Сообщение **4 8 15...** » 13 окт 2011, 16:08

ALEX165 писал(а):Source of the post
Не вникая во всё остальное - это, очевидно, неверно.
Даже у одной и той же системы со своим единственным лагранжианом может быть бесконечно много различных зависимостей r(t).

Да, спасибо. вот что-то такое я и ожидал. но то что бескон. много зависимостей r(t) у одной системы, и так понятно. всему причина - разные н.у.. а вот если в моей задаче начальные условия для обоих точек одинаковы: $r_1(0)=r_2(0), \dot{r}_1(0)=\dot{r}_2(0)$ , то все-таки разные зависимости?

ALEX165 · Сообщение **ALEX165** » 13 окт 2011, 16:13

4 8 15... писал(а):Source of the post
а вот если в моей задаче начальные условия для обоих точек одинаковы: $r_1(0)=r_2(0), \dot{r}_1(0)=\dot{r}_2(0)$ , то все-таки разные зависимости?

Если начальные условия одинаковые и лагранжианы одинаковые, то и r(t) будут идентичными, как пить дать!

4 8 15... · Сообщение **4 8 15...** » 13 окт 2011, 16:19

ALEX165 писал(а):Source of the post
Если начальные условия одинаковые и лагранжианы одинаковые, то и r(t) будут идентичными, как пить дать!

Тогда по движению второго шарика можно судить о движении первого. Тогда судя по потенциальной энергии второго первый,который вертится в плоскости в центрально-симметричном поле всегда должен падать на центр по спирали - но это же не так

peregoudov · Сообщение **peregoudov** » 13 окт 2011, 17:22

4 8 15... писал(а):Source of the post $P_\theta=Const=mr^2 \dot{\theta}~~=> L=\dfrac{m}{2}\dot{r}^2+\dfrac{P_\theta ^2}{2mr^2}-V(r).$

Ошибка в =>. Нельзя выражать скорости в лагранжиане, пользуясь законами сохранения. Сначала напишите уравнение Лагранжа для $$r$$

, а уж в нем исключайте скорость $\dot\phi$ --- получится правильно.

4 8 15... · Сообщение **4 8 15...** » 13 окт 2011, 17:51

peregoudov писал(а):Source of the post
4 8 15... писал(а):Source of the post $P_\theta=Const=mr^2 \dot{\theta}~~=> L=\dfrac{m}{2}\dot{r}^2+\dfrac{P_\theta ^2}{2mr^2}-V(r).$
Ошибка в =>. Нельзя выражать скорости в лагранжиане, пользуясь законами сохранения. Сначала напишите уравнение Лагранжа для , а уж в нем исключайте скорость $\dot\phi$ --- получится правильно.

О, спасибо! Так получается, что брать действие от такого "покалеченного" лагранжиана и искать траектории для реализации минимума уже не то... Теперь есть над чем хоть подумать

peregoudov · Сообщение **peregoudov** » 13 окт 2011, 17:58

Именно так. Нужно написать уравнение движения, исключить скорость с помощью закона сохранения, а потом восстановить по уравнению движения "редуцированный" лагранжиан.

yourdomain.com