офтоп
Не в меру развеселилась, со вчерашнего вечера. Действительно, только суровый профессиональный математик мог решить задачу №1 производящими функциями. Правда, он или недостаточно суров, или недостаточно профессионален. Надо было для определения к-та с помощью интегральной т-мы Коши вычеты посчитать.
Задача о лапах и общая постановка вопроса
Задача о лапах и общая постановка вопроса
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Юрий Олеша кутил в ресторане (видимо, допрокучивал гонорар за экранизацию "Трёх толстяков"). В какой-то момент он решил уходить, увидел человека в униформе, и между ними состоялся следующий диалог.Володиславир писал(а):Source of the post n = 6 просто не подходит к условию задачи.
О. - Официант, подайте такси.
А. - Я не официант, а адмирал.
О. -Тогда подайте катер!
Vlardenir, проверьте ваше решение для небольшого n, даже если вы адмирал.
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Проверила полученную формулу для n=2, 4, 6, 8, 10 и 306.
Количество разбиений подсчитывала с помощью программы))
Количество разбиений подсчитывала с помощью программы))
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Всё-таки накосячила. Простите слабомыслящую
...остаток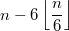 , набираемый двойками и четвёрками, равен или 0, или 2, или 4.
, набираемый двойками и четвёрками, равен или 0, или 2, или 4.
То есть случай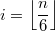 не надо рассматривать отдельно, если остаток равен 4, то общая формула дает для четвёрки 2 разбиения, а для 0 или 2 одно:
не надо рассматривать отдельно, если остаток равен 4, то общая формула дает для четвёрки 2 разбиения, а для 0 или 2 одно:
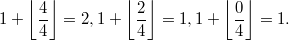
Теперь формула верна для всех чётных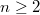 , что, конечно, радует))
, что, конечно, радует))
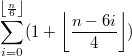
Хорошо бы её преобразовать и упростить, но пока не соображу, как.
ЗЫ. В предпредыдущем посте исправила, исправленному верить))
...остаток
То есть случай
Теперь формула верна для всех чётных
Хорошо бы её преобразовать и упростить, но пока не соображу, как.
ЗЫ. В предпредыдущем посте исправила, исправленному верить))
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Задача №2. Коммутативное разложение на двойки, тройки, четвёрки.
Сколько существует последовательностей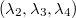 таких, что
таких, что 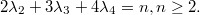
Буду делать аккуратно, чтобы не накосячить. Возможно, полученные формулы удастся объединить в одну.
Случай 1.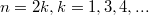
Количество троек в разбиении чётно, а именно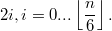
Если троек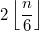 , то вклад троек в сумму равен
, то вклад троек в сумму равен 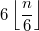 , остаток, набираемый двойками и четвёрками, равен
, остаток, набираемый двойками и четвёрками, равен 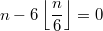 или
или 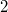 , или
, или 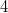 , разбиение существует, для 0 и 2 одно, для 4 - два.
, разбиение существует, для 0 и 2 одно, для 4 - два.
Для остальных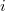 остаток
остаток 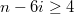 и чётен. Подсчитаем количество его разбиений на единицы и двойки.
и чётен. Подсчитаем количество его разбиений на единицы и двойки.
Т.к.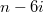 чётно, то количество разбиений на двойки и четвёрки равно количеству разбиений
чётно, то количество разбиений на двойки и четвёрки равно количеству разбиений 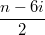 на единицы и двойки.
на единицы и двойки.
Отсюда общее количество разбиений равно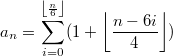 .
.
Сколько существует последовательностей
Буду делать аккуратно, чтобы не накосячить. Возможно, полученные формулы удастся объединить в одну.
Случай 1.
Количество троек в разбиении чётно, а именно
Если троек
Для остальных
Т.к.
Отсюда общее количество разбиений равно
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
Swetlana писал(а):Source of the post Vlardenir, проверьте ваше решение для небольшого n, даже если вы адмирал.
Так, у меня решение самое брутальное - тупым перебором.
И того q = 3
В общем, не понял
Наверное, Вы меня к чему-то подводите как бычка.
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
Swetlana: "С НОК-ом не поняла."
Так как с комбинаторикой знаком, лишь поверхностно, а будет правильно сказать, что не знаком, то задачку решал исключительно из своих соображений.
Получилось вот что:
Найти количество решений в целых числах у уравнения:
2x+3y+4z = 306 при x, y, z ≠ 0
По условию x, y, z ≠ 0 значит хотя бы по одному разу числа 2, 3, 4 входят в уравнение. Просумируем их 2+3+4 = 9 и вычтем из 306. Теперь будем иметь дело с числом 297.
Так как необходимо учесть все комбинации чисел 2, 3 и 4, то ищем НОК (наименьшее общее кратное) трёх чисел. Очевидно, что НОК(2, 3, 4) = 12.
Теперь можно найти все комбинации сумм для 12:
2+2+2+2+2+2
4+2+2+2+2
4+4+2+2
4+4+4
3+3+3+3
3+3+2+2+2
3+3+4+2
Имеем 7 комбинаций.
Далее, воспользуемся модульностью по НОК(2, 3, 4):
297 mod 12 = 9, т.е. получаем целочисленный остаток от деления на 12, и нужно найти комбинации для числа 9:
3+3+3
2+2+2+3
2+3+4
Имеем 3 комбинации.
Далее, вычитаем остаток 9 из 297 и делим на 12
(297-9)/12 = 24
Теперь остаётся подсчитать общее количество комбинаций чисел 2, 3, 4 для заданного уравнения:
Как-то так и получился частный случай с НОК( ).
Так как с комбинаторикой знаком, лишь поверхностно, а будет правильно сказать, что не знаком, то задачку решал исключительно из своих соображений.
Получилось вот что:
Найти количество решений в целых числах у уравнения:
2x+3y+4z = 306 при x, y, z ≠ 0
По условию x, y, z ≠ 0 значит хотя бы по одному разу числа 2, 3, 4 входят в уравнение. Просумируем их 2+3+4 = 9 и вычтем из 306. Теперь будем иметь дело с числом 297.
Так как необходимо учесть все комбинации чисел 2, 3 и 4, то ищем НОК (наименьшее общее кратное) трёх чисел. Очевидно, что НОК(2, 3, 4) = 12.
Теперь можно найти все комбинации сумм для 12:
2+2+2+2+2+2
4+2+2+2+2
4+4+2+2
4+4+4
3+3+3+3
3+3+2+2+2
3+3+4+2
Имеем 7 комбинаций.
Далее, воспользуемся модульностью по НОК(2, 3, 4):
297 mod 12 = 9, т.е. получаем целочисленный остаток от деления на 12, и нужно найти комбинации для числа 9:
3+3+3
2+2+2+3
2+3+4
Имеем 3 комбинации.
Далее, вычитаем остаток 9 из 297 и делим на 12
(297-9)/12 = 24
Теперь остаётся подсчитать общее количество комбинаций чисел 2, 3, 4 для заданного уравнения:
Как-то так и получился частный случай с НОК( ).
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Ха, проходит. Если в формулу для n подставить 0, то как раз одно разбиение и получится.
Хорошая формула , только непонятно, как её упростить.
Хорошая формула , только непонятно, как её упростить.
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Не поняла вашу формулу с НОКом, проверить ваше решение не могу. Проверка решения - дело рук самого решающего, для комбинаторных формул, во всяком случае. Я программу в делфях написала, себе не верю, все свои формулы проверяю. Вот сейчас (не веря своему доказательству и своему щастию, что и для нечётных n задача уже решена) проверила, до n=307. Совпадает ли тупой перебор для нечётного n с формулой числа разбиений чётного n-3. Совпадает.
Лемма.
Число разбиений
Доказательство.
У любого нечётного
Вот для n=3 не проходит. Для него есть одно разбиение, а для 0 разбиений нет.
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Количество коммутативных разбиений на двойки, тройки, четвёрки для любого натурального 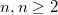 равно
равно
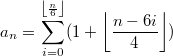 для чётного
для чётного 
и
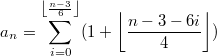 для нечётного
для нечётного 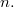
и
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Дискретная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость