Володиславир, просто не поняла, о чём вы спрашиваете. Гафу итегез))
Конечно, вычитаем 9 и для 297 решаем задачу в общем виде. Получается 1875.
Задача о лапах и общая постановка вопроса
Задача о лапах и общая постановка вопроса
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
α > 1.Володиславир писал(а):Source of the post То есть, в общем случае, этот результат верен для разбиений на единицы и с коэффициентом α?
Последний раз редактировалось Swetlana 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
Всё-таки НОК не даёт покоя
Так как большинство странных мыслей приходит ночью, то за правильность не особо ручаюсь.
Наверное с помощью НОК(a,b) можно выразить количество разбиений числа n, суммами чисел а и b.
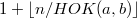 при n - чётное;
при n - чётное;
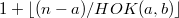 при n - не чётное
при n - не чётное
Но при условиях достаточно больших n и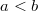
Достаточно большое n означает, что оно превышает последнее не выражаемое число суммой чисел a и b.
Так для пары 5 и 7, последним не выражаемым числом будет 23.
Так как большинство странных мыслей приходит ночью, то за правильность не особо ручаюсь.
Наверное с помощью НОК(a,b) можно выразить количество разбиений числа n, суммами чисел а и b.
Но при условиях достаточно больших n и
Достаточно большое n означает, что оно превышает последнее не выражаемое число суммой чисел a и b.
Так для пары 5 и 7, последним не выражаемым числом будет 23.
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
Нашёл формулы для последних не выражаемых чисел, суммами чисел a и b. Обозначу это число как  Здесь так же два случая:
Здесь так же два случая:
1) Когда а и b одновременно не чётные числа или одно число чётно, другое не чётно. Тогда формула выглядит:

2) Когда а и b одновременно чётные числа:

Тогда дополнительные (все?) не выражаемые числа можно найти простым последовательным вычитанием из комбинаций чисел а и b.
комбинаций чисел а и b.
Люди, ау! Кто-нить, может я тут велосипед изобретаю, увлекательно конечно, но может есть где об этом прочитать? Плюс время сэкономиться.
1) Когда а и b одновременно не чётные числа или одно число чётно, другое не чётно. Тогда формула выглядит:
2) Когда а и b одновременно чётные числа:
Тогда дополнительные (все?) не выражаемые числа можно найти простым последовательным вычитанием из
Люди, ау! Кто-нить, может я тут велосипед изобретаю, увлекательно конечно, но может есть где об этом прочитать? Плюс время сэкономиться.
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
Эх, никто так и не подсказал, а литература-то есть.
Г.Эндрюс "Теория разбиений". (1982)
Г.Эндрюс "Теория разбиений". (1982)
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
А можно ли получить формулу в закрытом виде?Swetlana писал(а):Source of the post Количество коммутативных разбиений на двойки, тройки, четвёрки для любого натурального n, n\geq 2 равно a_{n} = \sum_{i=0}^{\left \lfloor\frac{n}{6} \right \rfloor }(1+\left \lfloor \frac{n-6i}{4} \right \rfloor) для чётного n и a_{n} = \sum_{i=0}^{\left \lfloor\frac{n-3}{6} \right \rfloor }(1+\left \lfloor \frac{n-3-6i}{4} \right \rfloor) для нечётного n.
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
Упростить не удасться. Данная форма, видимо, наиболее простая.Swetlana писал(а):Source of the post \sum_{i=0}^{\left \lfloor\frac{n}{6} \right \rfloor }(1+\left \lfloor \frac{n-6i}{4} \right \rfloor) Хорошо бы её преобразовать и упростить, но пока не соображу, как.
А перевести ряд в закрытую форму, т.е. в обычную формулу можно. Выкладки приводить не буду, если заинтересуетесь как получилось дайте знать.
Результат в общем виде следующий:
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Задача о лапах и общая постановка вопроса
Последний раз редактировалось grigoriy 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
- Володиславир
- Сообщений: 122
- Зарегистрирован: 28 окт 2015, 21:00
Задача о лапах и общая постановка вопроса
"Нам помогут только массовые расстрелы" (с)grigoriy писал(а):Source of the post ...
Может заглянет.
Однако, исправил формулу на неправильную, но сейчас обнаружил, что и прежняя хоть и давала правильный результат по условиям задачи, но в общем случае тоже не верна. К тому же, сама метода вывода, мало содержательна по отношению к комбинаторике.
В общем, я в депрессии.
Последний раз редактировалось Володиславир 27 ноя 2019, 18:54, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Дискретная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость