Вычислить мощность множества |T0 ∩ T1 U L ∩ S|
Подскажите, пожалуйста.
Мощность множества
-
loginlogin
- Сообщений: 2
- Зарегистрирован: 19 июн 2014, 21:00
Мощность множества
Последний раз редактировалось loginlogin 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
по моему недостаточно информации
Последний раз редактировалось folk 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
Последний раз редактировалось Sonic86 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
Заданная размерность n подразумевается, указанные множества определяются только при известном n
Ответ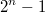 -столько же сколько и линейных самодвойственных
-столько же сколько и линейных самодвойственных
UPD: вот она привычка к ликсу где фигурные скобки не нужны.Конечно ответ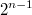
Линейные -это свободный выбор n бинарных коэффициентов при переменных,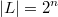
Самодвойственные среди линейных - число коэффициентов =1 нечетно. Разложение бинома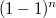 показывает, что их ровно половина.Ну и в этом случае они все будут и в
показывает, что их ровно половина.Ну и в этом случае они все будут и в 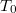 и в
и в 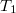
Где ошибка?
Ответ
UPD: вот она привычка к ликсу где фигурные скобки не нужны.Конечно ответ
Линейные -это свободный выбор n бинарных коэффициентов при переменных,
Самодвойственные среди линейных - число коэффициентов =1 нечетно. Разложение бинома
Где ошибка?
Последний раз редактировалось Ian 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
Вычислить мощность множества
Подскажите, пожалуйста.
Последний раз редактировалось Sonic86 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
Ian писал(а):Source of the post
Заданная размерность n подразумевается, указанные множества определяются только при известном n
Ответ-столько же сколько и линейных самодвойственных
Крайний раз думал над вашим ответом два дня, похоже рекорд побьем на этот раз
Последний раз редактировалось folk 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
Потратьте это время на чтение хоть самых основ
Последний раз редактировалось Ian 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
Офигеть, Ian просто великолепен!
Последний раз редактировалось mihailm 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
А я вот сомневаюсь в решении
По порядку - классы функций видны сразу, понятно что множество как-то фиксировано, логично предположить что это все n-местные ф-ии.
А вот дальше - какой порядок действий? Логично предположить, что порядок объединений/пересечений аналогичен дизъюнкции/конъюнкции. Но тогда
Извиняюсь, только сейчас заметил редактуру поста. Стало немного яснее, но ...
Первое, количество линейных
А вот искомое число можно оценить так, всего n-местных функций
Последний раз редактировалось СергейП 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Мощность множества
На беглый взгляд получается 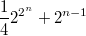 , что похоже на правду при
, что похоже на правду при 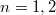
При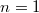 у нас всего
у нас всего 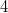 функции, из которых ровно две (
функции, из которых ровно две ( и
и 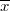 ) принадлежат искомому множеству...
) принадлежат искомому множеству...
А почему не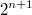 ?
?
Хм, да. Только не учтены функции со "свободным членом".
Но, во всяком случае, в пересечении последних классов функций гораздо больше.
upd: СергейП опередил немного
При
Ian писал(а):Source of the post
Линейные -это свободный выбор n бинарных коэффициентов при переменных,
А почему не
Хм, да. Только не учтены функции со "свободным членом".
Но, во всяком случае, в пересечении последних классов функций гораздо больше.
upd: СергейП опередил немного
Последний раз редактировалось YURI 27 ноя 2019, 19:20, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Дискретная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 1 гость