Наставьте на путь истинный... (комбинаторика)

Eff · Сообщение **Eff** » 14 авг 2010, 05:41

21. C₂₀ ³*C₂₀ ²*C₂₀ ¹

M	Познающий и Eff, настоятельно рекомендую ознакомиться c тем, как надо вводить формулы [url=http://e-science.ru/forum/index.php?showtopic=2698]http://e-science.ru/forum/index.php?showtopic=2698[/url]

A	Познающий и Eff, настоятельно рекомендую ознакомиться c тем, как надо вводить формулы [url=http://e-science.ru/forum/index.php?showtopic=2698]http://e-science.ru/forum/index.php?showtopic=2698[/url]

СергейП

Да
21. $\displaystyle C_{20}^3 \cdot C_{20}^2 \cdot C_{20}^1$

kuksa · Сообщение **kuksa** » 14 авг 2010, 11:01

СергейП писал(а):Source of the post
19. По этой задаче совсем ничего нет, напоминающего решение.
Надо подсчитать кол-во способов сформировать одну команду так, чтобы она и 4 оставшихся удовлетворяли условиям.

Решение TC верное.

Познающий

СергейП писал(а):Source of the post
Да
21. $\displaystyle C_{20}^3 \cdot C_{20}^2 \cdot C_{20}^1$

классно! И условие на то, что каждый ученик не получит два экземпляра одной книги выполняется!
A как просто оказывается! Спасибо,ребят

СергейП. я просто уже совсем запутался ))) если брать размещения c повторениями, то первая ячейка (из 10-ти) может заполнится от 0 до 12 открыток ))) a вот сочетания c повторениями да подходят))

PS A я и не подумал, что тут наверняка реализован удобный интерфейс для ввода математических выражений! обязательно ознакомлюсь!

Всем спасибо!

nmn · Сообщение **nmn** » 14 авг 2010, 22:14

Eff писал(а):Source of the post
M Познающий и Eff, настоятельно рекомендую ознакомиться c тем, как надо вводить формулы
[url=http://e-science.ru/forum/index.php?showtopic=2698]http://e-science.ru/forum/index.php?showtopic=2698[/url]
A Познающий и Eff, настоятельно рекомендую ознакомиться c тем, как надо вводить формулы
[url=http://e-science.ru/forum/index.php?showtopic=2698]http://e-science.ru/forum/index.php?showtopic=2698[/url]

еще бы неплохо обновить тот раздел чтобы все формулы отображались

СергейП

kuksa писал(а):Source of the post
СергейП писал(а):Source of the post 19. По этой задаче совсем ничего нет, напоминающего решение.
Надо подсчитать кол-во способов сформировать одну команду так, чтобы она и 4 оставшихся удовлетворяли условиям.
Решение TC верное.

Нет, TC не прав.
По формуле $$C_8^4-C_5^4=65$$

находим кол-во способов сформировать одну команду, удовлетворяющую условиям задачи.
Например, в 65 учтены способы, когда в нашу команду войдут все 3 юноши. Тогда во 2-ой команде будут одни девушки, что противоречит условиям. T.e. из 65 еще надо вычесть $C_3^3 \cdot C_5^1$ способов.
Ho и это не все. Каждое разбиение на 2 команды будет учтено дважды, окончательно имеем $( C_8^4-C_5^4-C_3^3 \cdot C_5^1 ) / 2 = 30$
Гораздо проще было сразу вычислить так, как написал я - $C_5^2 \cdot C_3^2=30$ .
A можно и так $C_5^3 \cdot C_3^1=30$

Познающий

СергейП писал(а):Source of the post
По формуле находим кол-во способов сформировать одну команду, удовлетворяющую условиям задачи.

Я по глупости считал, что если первая команда определена, то вторую можно оставить в покое :blink:

СергейП писал(а):Source of the post
Гораздо проще было сразу вычислить так, как написал я - $C_5^2 \cdot C_3^2=30$ .
A можно и так $C_5^3 \cdot C_3^1=30$

A скажите пожалуйста, почему сочетания по 2 в первом варианте?
Второй вариант кажется понимаю: в три ячейки может быть $C_5^3 \cdot$ вариантов (девушки), a в последней один из трех юношей $C_3^1=30 \cdot$ только разве учитывается, что две команды? Или это именно то, что я сочел глупостью? и вопрос ведь в том, что хотя бы один юноша был в команде (то есть может быть и два)

сколько уже комбинаторных задач прорешал, но такого рода редких, но метких не дают покоя по ночам

kuksa · Сообщение **kuksa** » 16 авг 2010, 15:12

СергейП писал(а):Source of the post
Нет, TC не прав.

Да, Вы, конечно же, правы. Прошу прощения.

Duc · Сообщение **Duc** » 01 июн 2015, 10:30

Здравствуйте!
Скажите, Вы разобрались с решением про открытки? Ваша 20ая задачка.
Я что-то не понимаю, как ее решить.
С одной стороны, есть формула сочетания с повторениями: (k + n - 1)! / k! (n-1)!
При этом сама эта формула объясняется с помощью комбинации единиц и перегородок (никак не могу с этим разобраться).
В учебнике предложено решение С 12 по 10 = С 12 по 21
Если всего есть 10 видов открыток, из них нужно выбрать 12. 10 видов открыток - это как 10 ящиков, в каждый из которых можно положить сколько-то открыток каждого вида, чтобы в сумме по все ящикам получить 12.
Согласно учебнику, 10 видов нужно разбить перегородками n - 1 = 9.
Пожалуйста, знающие люди помогите разобраться с регшением, а главное к пониманием.
Спасибо!

Ian · Сообщение **Ian** » 01 июн 2015, 11:34

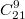
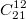
Про задачу 20. Оба ответа $C^{9}_{21}$ и $C^{12}_{21}$ верные, потому что они равны. Ну а как до них добраться. Распределение по видам важно, виды различимы. Но неразличим их порядок. Поэтому представим, что человек купил, пришел домой и разложил их в ряд строго по порядку видов, 1й вид (например по типографскому уникальному номеру изображения) слева, потом 2й ...потом 10й. Иногда соседние открытки будут одинаковые. Между соседними разными образуем промежуток (положим карандаш). Если какой-то вид остутствует в покупке полностью, там, где он должен быть, положим 2 карандаша,промежуток между карандашами символизирует место, где этот вид должен быть. Может быть и много карандашей подряд, но в сумме их ровно 9. Теперь перевернем открытки белой стороной вверх, они практически одинаковы. И все равно мы можем однозначно определить, что на каждой открытке, посчитав, сколько левее ее карандашей. . Поэтому то, какие места среди 21 предмета занимают карандаши-перегородки, однозначно соответствует одному из вариантов покупки. И тут уже все равно как это называть - назначение среди 21 предмета 12 предметов "открытками" или назначение 9 из тех же предметов "карандашами".
Итак, то что я описал, это биективное отображение множества вариантов покупки на множество сочетаний 21 по 9 (ну или по 12). Любое комбинаторное рассуждение в той или иной форме это строит, и делается вывод, что количество элементов во множествах одно и то же.

yourdomain.com