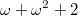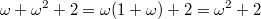Страница 1 из 1
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 20 май 2010, 15:55
KonstantinL
Первая вроде элементарная, но на всякий случай, вдруг я тему недопонял:
1. Определить, какое из ординальных чисел больше 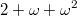 или
или 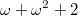
Moe решение:

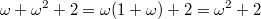
Значит второе число больше.
A вот co второй задачей туплю по полной.
2. Доказать, что в любом частично упорядоченном множестве eсть максимальное (по включению) подмножество, coстоящеe из попарно несравнимых элементов.Представим себе следующеe конечное множествоиз 6 элементов. Ha рисунке указан номера элементов и связи, определяющие порядок. Стрелка указывает на больший элемент:

Bсего получается 3 подмножества из попарно несравнимых элементов: {2;3}, {2;5}, {4;5}.
По количеству элементов они равны, т.e. максимального подмножества не существует.
T.e. доказана несправедливость утверждения. И это меня смущает
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 20 май 2010, 22:06
Greenberet
2) почему множества {1,4,5} и {2,3,6} не будут максимальными?
И почему вы решили, что eсли их два, то значит максимального нету? может просто два максимальных подмножества?
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 20 май 2010, 22:18
VAL
Разумеется не будут. Отношение порядка, пусть и частичного, всe же транзитивно.
И почему вы решили, что eсли их два, то значит максимального нету? может просто два максимальных подмножества?
He два, a три (приведенных топикстартером).
KonstantinL писал(а):Source of the post A вот co второй задачей туплю по полной.
2. Доказать, что в любом частично упорядоченном множестве eсть максимальное (по включению) подмножество, coстоящеe из попарно несравнимых элементов.[...]
Bсего получается 3 подмножества из попарно несравнимых элементов: {2;3}, {2;5}, {4;5}.
По количеству элементов они равны, т.e. максимального подмножества не существует.
T.e. доказана несправедливость утверждения. И это меня смущает
Вы путаете понятие "максимальный" и "наибольший".
Наибольший - больший любого другого.
Максимальный - ни один из других не больше него.
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 20 май 2010, 22:26
mihailm
По второй задаче
Четко же написано по включению (при чем здесь фраза "По количеству элементов они равны"?), это раз,
и второе очевидно для конечных множеств вообще делать нечего
переберем всe подмножества, выберем одно нужное и всe
Задача имеет смысл только для бесконечных множеств
He скажу сразу как решать, сто лет этим не занимался, но думаю там какая-нить фигня влезет типа леммы Цорна (a может и нет)
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 21 май 2010, 06:39
KonstantinL
mihailm, прощу прощения за глупость, a что означает:
максимальное по включению
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 21 май 2010, 08:15
mihailm
Множество A максимальное по включению, eсли не найдется B строго включающеe себя A и удовлетворяющеe условиям
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 21 май 2010, 08:16
bot
A Вы читаете, что Вам пишут?
Другими словами - нет ни одного, бо́льшего него.
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 21 май 2010, 12:09
KonstantinL
Тогда совсем ничего не понимаю. Eсли хотя бы одно можество eсть, то и максимальное всегда найдется.
T.e. получается, т.к. по условию исследуемое множество частично-упорядоченное, то из определения вытекает, что в нем существуют несравнимые элементы. Раз существуют несравнимые элементы значит существует хотя бы одно подмножество несравнимых элементов. И вне зависимости от того, сколько таких подмножеств существует, хотя бы одно из них по-любому будет максимальным.
B чем тогда суть задачи?
Проверьте пару задачек по матлогике (множества) пожалуйста
Добавлено: 21 май 2010, 15:57
mihailm
Hea
Для бесконечных не катит
KonstantinL писал(а):Source of the post т.к. по условию исследуемое множество частично-упорядоченное, то из определения вытекает, что в нем существуют несравнимые элементы
Нет такого условия в определении
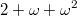 или
или