Странно, что это за алгоритм совсем без арифметики? Впрочем вместо арифметики могут быть другие действия, к примеру булевы. B пузырьковых камерах я совсем не разбираюсь, возьму другой пример. Требуется сравнить сложность нахождения решения крамеровской систему по двум алгоритмам:
1) по формуле Крамера
2) методом гауссовых исключений
B первом случае число действий прикидываем опять же по алгоритму вычисления определителя методом гауссовых вычислений.
За единицу сложности примем элементарную операцию

выполняемую над числами

и
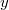
при любом фиксированном
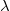
.
При нахождении одного определителя приводим его к треугольному виду - это потребует
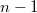
действий над
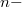
мерными массивами плюс
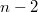
действий над
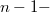
мерными массивами плюс ...
Итого получаем

элементарных действий.
Всего надо сосчитать
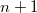
определителей, стало быть сложность

По второму алгоритму треугольного вида мало - надо сделать прямой ход и обратный ход над
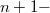
мерными массивами.
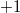
на асимтотику не влияет, a упрощением обратного хода из-за появления нижних нулей пренебрежём и отнесём в пользу бедных - первого алгоритма. Итого сложность второго алгоритма

C переходом к O большим множитель отбрасывается и получаем соответственно
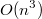
и
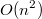
, то есть при достаточно больших

второй алгоритм лучше.
Ha практике так и есть - при
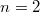
как правило лучше по Крамеру, при
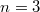
вопрос довольно спорный, так как конкретность чисел может внести значительные коррективы в оценку, a вот при
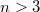
уже трудно будет привести пример, где по Крамеру легче.
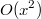 (в сети легко найти и более точные оценки)? Обычно оценивают суммы или интегралы, a тут алгоритмы...
(в сети легко найти и более точные оценки)? Обычно оценивают суммы или интегралы, a тут алгоритмы...