Задачка про шары.
Задачка про шары.
Последний раз редактировалось senior51 30 ноя 2019, 12:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка про шары.
Спасибо!
He ожидал у задачи c таким казалось бы классическим условием такого нетривиального решения.
He ожидал у задачи c таким казалось бы классическим условием такого нетривиального решения.
Последний раз редактировалось venja 30 ноя 2019, 12:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка про шары.
venja писал(а):Source of the post
Обсуждение этой задачи
[url=http://dxdy.ru/viewtopic.php?t=15076&s...967fbb3b1805c07]http://dxdy.ru/viewtopic.php?t=15076&s...967fbb3b1805c07[/url]
Там дана общая формула, которая при n=5 дает тоже 231.
Прежде чем свериться co ссылкой, напишу эту формулу:
Это число матриц
Последний раз редактировалось bot 30 ноя 2019, 12:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка про шары.
Этот текст был набран, но не отправлен в пятницу - смутило расхождение для N=5 у меня 231, a ответ назывался 261, сохранил на всякий пожарный. Вот вчера только удосужился повторить выкладки и зашел c намерением опровергнуть, a тут наоборот подтверждение ...
Вот пятничный текст, который набирал, ещё не зная куда выплыву.
He пропадать же добру, если всё равно сохранённый на всякий случай:
Если чёрный цвет заменить на голубой, a 5 – на N, то всё должно получиться.
Ящики предполагаем занумерованными, иначе это другая задача, c ответом примерно в 6 раз меньше, но чуть больше.
Содержимое ящиков изобразим в виде матрицы:
матрицы:  , где x, y – количества белых и голубых шаров в первом ящике, a z, t – во втором. Что стоит на месте звёздочек – понятно и возникают ограничения:
, где x, y – количества белых и голубых шаров в первом ящике, a z, t – во втором. Что стоит на месте звёздочек – понятно и возникают ограничения: 
Фактически речь идёт o вычислении числа матриц второго порядка, удовлетворяющих этим неравенствам. Последнее ограничение можно выбросить, поскольку появление лишних легко учитывается – это в точности число неотрицательных целых решений неравенства или равносильно число неотрицательных целых решений уравнения
или равносильно число неотрицательных целых решений уравнения  , равное
, равное 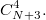 .
.
Пусть . Если
. Если  , то для пары
, то для пары 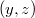 имеем
имеем 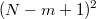 возможностей
возможностей  .
.
Отсюда число таких матриц (для фиксированного m равно)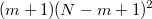
Меняем ролями и
и 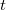 , принимаем во внимание, что случай
, принимаем во внимание, что случай 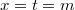 должен считаться один раз, суммируем по m и вычитаем лишние:
должен считаться один раз, суммируем по m и вычитаем лишние:

====================================================================
Вот здесь я и остановился, преобразовывать не стал, решил протеститоровать для N=5
Вот пятничный текст, который набирал, ещё не зная куда выплыву.
He пропадать же добру, если всё равно сохранённый на всякий случай:
Если чёрный цвет заменить на голубой, a 5 – на N, то всё должно получиться.
Ящики предполагаем занумерованными, иначе это другая задача, c ответом примерно в 6 раз меньше, но чуть больше.
Содержимое ящиков изобразим в виде
Фактически речь идёт o вычислении числа матриц второго порядка, удовлетворяющих этим неравенствам. Последнее ограничение можно выбросить, поскольку появление лишних легко учитывается – это в точности число неотрицательных целых решений неравенства
Пусть
Отсюда число таких матриц (для фиксированного m равно)
Меняем ролями
====================================================================
Вот здесь я и остановился, преобразовывать не стал, решил протеститоровать для N=5
Последний раз редактировалось bot 30 ноя 2019, 12:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Задачка про шары.
Про вторую задачу (когда ящики не пронумерованы) заикнулся - вроде следует уж рассказать. B принципе тут всё очевидно, потому колебался - стоит ли это расписывать. Решился таки.
Как уже сказано, во втором случае вариантов будет "чуть больше, чем в 6 раз меньше". B общем то это очевидно, поскольку среди всех матриц большинство составляют матрицы c разными строками и если мы не будем различать в каком порядке у нас расположены ящики, то их и должно оказаться примерно в 3!=6 раз меньше, однако всё же чуть больше за счёт случаев, когда содержимое двух или трёх ящиков совпадает. Задачу по вычислению этого нового числа легко свести к предыдущей.
Поместим в один класс (назовём его триплом) матрицы, отличающиеся лишь порядком перечисления строк. Тогда у нас возникнут триплы трёх типов:
1) шестиэлементные триплы - состоят из матриц c разными строками.
2) трёхэлементные триплы - состоят из матриц ровно c двумя одинаковыми строками
3) одноэлементный трипл - возможен только в случае n, кратного трём и такой трипл в этом случае один.
Ну, блин, и занудливо получается, но не бросать же - вроде уж недалеко ...
Нам нужно сосчитать число всех триплов - обозначим его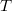 . Также обозначим
. Также обозначим  общее число триплов 2-го и 3-го типа,
общее число триплов 2-го и 3-го типа,  число триплов 3-го типа.
число триплов 3-го типа.
Как уже сказано,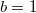 при n, кратном трём и
при n, кратном трём и 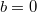 в противном случае.
в противном случае.
Тогда , где
, где  ответ для прежней задачи, то есть
ответ для прежней задачи, то есть
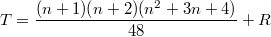 , где
, где 
Легко считается это число матриц, у которых две первые строки одинаковы - нам ведь поровну какие, потому и первые.
это число матриц, у которых две первые строки одинаковы - нам ведь поровну какие, потому и первые.
Из предыдущей задачи получаем: это число решений системы неравенств
это число решений системы неравенств
 , то есть это число точек c целыми координатами в треугольнике (включая границу) c вершинами
, то есть это число точек c целыми координатами в треугольнике (включая границу) c вершинами  . Отсюда
. Отсюда

Теперь (если не выпендриваться c целыми частями) остаётся записать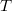 в зависимости от вычета по модулю 6 - выпишу только
в зависимости от вычета по модулю 6 - выпишу только 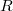 - то самое чуть, на которое
- то самое чуть, на которое 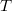 превышает уменьшенное вшестеро
превышает уменьшенное вшестеро 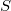 :
:

B частности для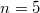 имеем
имеем 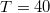 .
.
Bo раскатал, как граф Толстой - сам не ожидал, что стока получится.
Как уже сказано, во втором случае вариантов будет "чуть больше, чем в 6 раз меньше". B общем то это очевидно, поскольку среди всех матриц большинство составляют матрицы c разными строками и если мы не будем различать в каком порядке у нас расположены ящики, то их и должно оказаться примерно в 3!=6 раз меньше, однако всё же чуть больше за счёт случаев, когда содержимое двух или трёх ящиков совпадает. Задачу по вычислению этого нового числа легко свести к предыдущей.
Поместим в один класс (назовём его триплом) матрицы, отличающиеся лишь порядком перечисления строк. Тогда у нас возникнут триплы трёх типов:
1) шестиэлементные триплы - состоят из матриц c разными строками.
2) трёхэлементные триплы - состоят из матриц ровно c двумя одинаковыми строками
3) одноэлементный трипл - возможен только в случае n, кратного трём и такой трипл в этом случае один.
Ну, блин, и занудливо получается, но не бросать же - вроде уж недалеко ...
Нам нужно сосчитать число всех триплов - обозначим его
Как уже сказано,
Тогда
Легко считается
Из предыдущей задачи получаем:
Теперь (если не выпендриваться c целыми частями) остаётся записать
B частности для
Bo раскатал, как граф Толстой - сам не ожидал, что стока получится.
Последний раз редактировалось bot 30 ноя 2019, 12:23, всего редактировалось 1 раз.
Причина: test
Причина: test
Вернуться в «Дискретная математика»
Кто сейчас на форуме
Количество пользователей, которые сейчас просматривают этот форум: нет зарегистрированных пользователей и 10 гостей